2022-2022数学周报七年级人教版相交线与平行线阶段性测试题答案

10.解:(1)设N(4,y),代入x2=2py、a9所以|M/≈8NF|=2+y=由题设得2++2=}×解得p=-2(舍去)或p=2,所以C的方程为x2=4y(6分)(2)由题知直线l的斜率存在,设其方程为y=kx+6kr+6由消去y整理得x2-4kx-24=0=4y显然△=16k2+96>0设P(x1y)Q(x2,y2),4k则C1·x224.抛物线在点P(x,)处的切线方程为y-耳x一x1)令y=-1,得x≈x-4可得点R由Q,F,R三点共线得k=k,rE1所以x-42即(x-4)(x2-4)+16x1x2=0,整理得(x1x2)2-4[(x+x2)2-2x1x2]+16+16xx=0,所以(-24)2-4[(4k)2-2×(-24)]+16+16×(-24)=0,解得k-子,即k一士,故所求直线l的方程为y=1x+6或y=-1x+(20分)

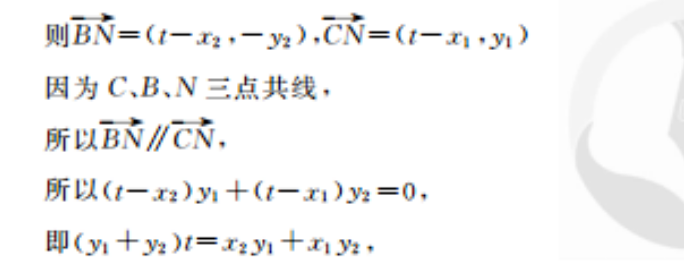
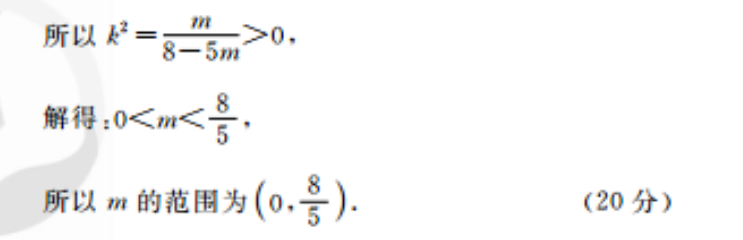
11.解:(1)由椭圆的焦点在x轴上,设椭圆C的方程为+=1(a>b>0),椭圆C的一个顶点为(0,1),即b=1.由=一√-(÷)一若解得a2=5,所以椭圆C的标准方程为+y2=1.(6分)(2)由题得F(2,0),设A(x1,y1),B(x2,y2),设直线l的方程为y=k(x-2)(k≠0),代入椭圆方程,消去y可得(5k2+1)x2-20k2x+20k2-5=0,则x1+x2=3220k2-5x1x=5k2+1因为点C与点A关于x轴对称∴C(x1,-y1)假设存在N(,0),使得C、B、N三点共线,则BN=(1-n2,-y2),N=(1-x1,y)因为C、B、N三点共线,所以BN∥CN,所以(-x2)y+(t-x1)y2=0即(y1+y2)t=x2y+x1y2,所以t=(x1=2)x2+kx=2)x(x1-2)+k(x2-2)2xx2-2(x1+x2)tIz20k20k5k2+152·220k52+1-4所以存在定点(号,0)使得CB、N三点共线(14分)(3)由0≤m≤2,MA+MB=(x+x2-2m,y+y2),AB=(x2-x,y2-y)因为(MA+MB⊥AB所以(M+MB)·AB=0,所以(x1+x2-2m)(x2-x1)+(y2-y1)(y1+y2)0所以20k5k2+15k2+10所以k8-50解得:0

以上就是2022-2022数学周报七年级人教版相交线与平行线阶段性测试题答案，更多英语周报答案请关注本网站。