数学周报2022-2022八上第3期答案

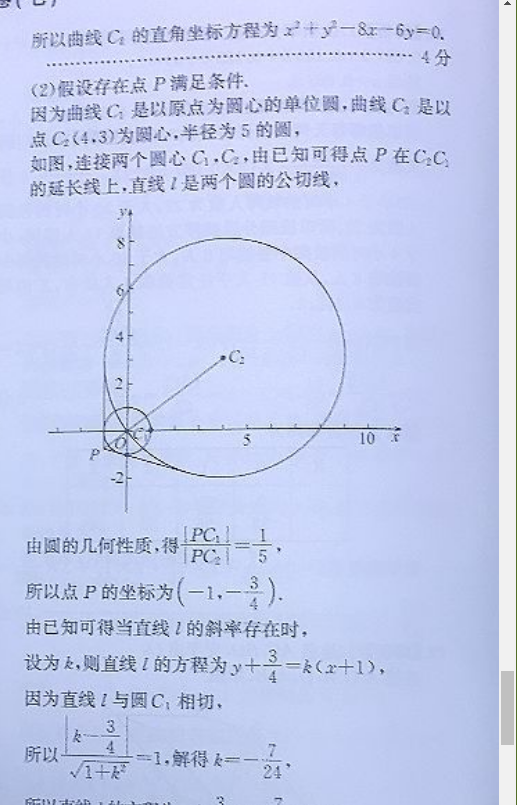
22.【解析】(1)由y=1e平方相加得x2+y所以曲线C的普通方程为十y=1…2分由=80a+6sna两边都乘以p得p=8a+opsin a,所以x2+y2=8x+6y,所以曲线C的直角坐标方程为x2+y2-8x-6y=0.4分(2)假设存在点P满足条件因为曲线C1是以原点为圆心的单位圆,曲线C2是以点C2(4,3)为圆心,半径为5的圆,如图,连接两个圆心C1,C2,由已知可得点P在C2C的延长线上,直线l是两个圆的公切线,由圆的几何性质,得所以点P的坐标为(-1,一3由已知可得当直线l的斜率存在时,设为k,则直线的方程为y+=k(x+1),因为直线l与圆C1相切,所以1+1,解得k=一224所以直线的方程为y+3=-2(x+1)即24y+7x+25=0,……………………8分当直线l的斜率不存在时,方程为x=-1.所以存在点P(-1,-4),使得过点P的直线!与曲线C1只有一个公共点时,必与C2只有一个公共点,直线l的方程为x=-1,或7x+24y+25=0.…10分

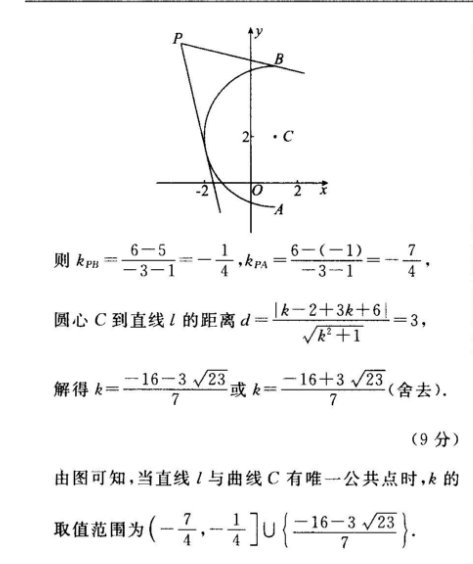
22.解:(1)当a2+kπ(k∈Z)时,x=-3;(1分=-3+tcos a当a≠+k(k∈Z)时,由消去参y=6-Ttsin a数t,得直线l的普通方程为 rtan a-y+3tana+6=0(3分)将x2+y2=p2,x= pcos 6,y=psin6代入p22p(cos0+2sin0)=4(其中pcos0≤1),得曲线C的直角坐标方程为(x-1)2+(y-2)2=9(x≤1).(5分)(2)设k=tana,则直线l的方程为y=k(x+3)+6,它表示过定点P(-3,6)的直线,由(1)可知,曲线C表示以点(1,2)为圆心,半径为3的半圆,如下图所示,其中A(1,-1),B(1,5)则k。=6-56-(-1)圆心C到直线l的距离d=12+3k+6解得k=-16-323或k==16+3√(舍去)(9分)由图可知,当直线l与曲线C有唯一公共点时,k的取值范围为(-,-]u16-37综上所述,ma的取值范围为(-x,-4]U16(10分):

以上就是数学周报2022-2022八上第3期答案，更多英语周报答案请关注本网站。