2020~2022《数学周报》八年级上册答案

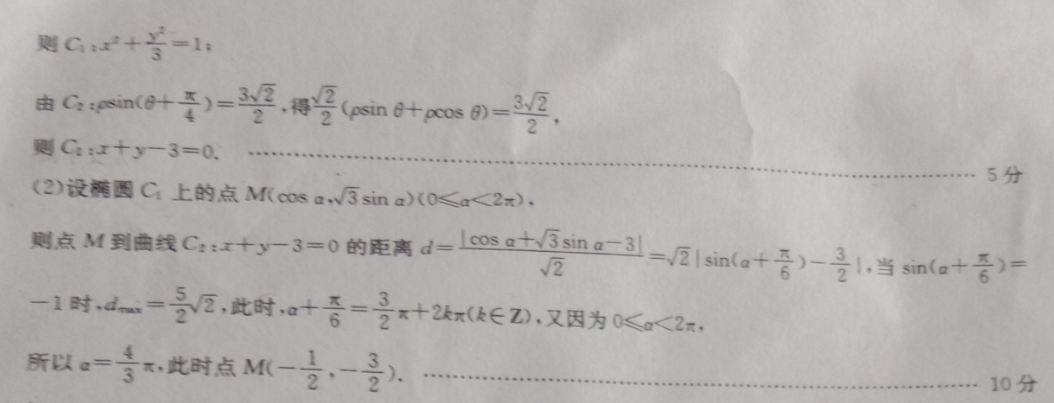
22.解:本题考查极坐标及参数方程cos r-rT- cOs(1)由C(为参数),可得{sm=2又sm+=1y=v3sin则由C0+)=32,得号(m时+sB=22则C3=05分(2)设椭圆C上的点M(cosa,3sina)(0≤a<2x),则点M到曲线C:x+y-3=0的距离d=1+sng-3l=2sm(a+)-3√21,当sin(a+÷)1时、d=5、,此时、+飞二3x+2kx(k∈D,又因为0≤a<2x所以。=1x此时点M(-1,-3……10分

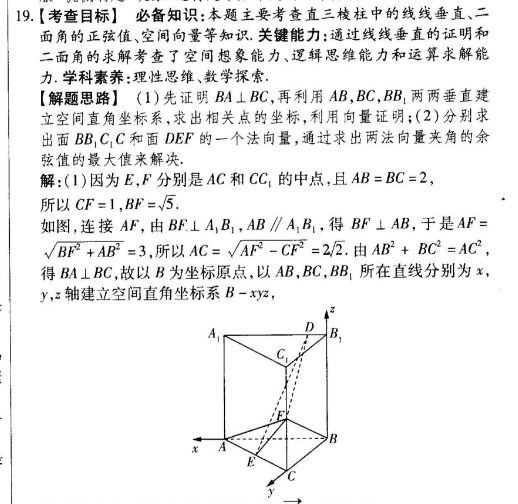
19.【考查目标】必备知识:本题主要考查直三棱柱中的线线垂直、二面角的正弦值、空间向量等知识.关键能力:通过线线垂直的证明和二面角的求解考查了空间想象能力、逻辑思维能力和运算求解能力学科素养:理性思维、数学探索【解题思路】(1)先证明BA⊥BC,再利用AB,BC,BB1两两垂直建立空间直角坐标系,求出相关点的坐标,利用向量证明;(2)分别求出面BB1C1C和面DEF的一个法向量,通过求出两法向量夹角的余弦值的最大值来解决解:(1)因为E,F分别是AC和C1的中点,且AB=BC=2所以CF=1,BF=√5.如图,连接AF,由BF⊥A1B1,AB∥AB,得BF⊥AB,于是AF=BF+ABF=3,所以AC=√AF-CF=2.由AB2+BC2=AC2,得BA⊥BC,故以B为坐标原点,以AB,BC,B1所在直线分别为x,y,z轴建立空间直角坐标系B-xy则B(0,0,0),E(1,1,0),F(0,2,1),BF=(0,2,1)设B1D=m(0≤m≤2),则D(m,0,2),于是DE=(1-m,1,-2)所以B.DE=0,所以BF⊥DE(2)易知面BB1C1C的一个法向量为n1=(1,0,0)设面DFE的法向量为n2=(x,y,2),n,又靂=(1-m,1,-2),E=(-1,1,1)所以(1-m)x+y-2z=0-x+y+z=0,令x=3,得y=m+1,z=2-m,于是,面DFE的一个法向量为n2=(3,m+1,2-m),所以cos(n1,n2〉=)2设面BCC与面DFE所成的二面角为6,则in6=√1-m(n1,m2),故当m=时,面BBCC与面DFE所成的二面角的正弦值最小为,即当B1D=时,面BB1C1C与面DFE所成的二面角的正弦值最小.【解題关键】本题求解关键是建立恰当的空间直角坐标系,确定相关点的坐标,再利用空间向量进行运算

以上就是2020~2022《数学周报》八年级上册答案，更多英语周报答案请关注本网站。