数学周报易学通人教a版2020－2021选修1－1答案

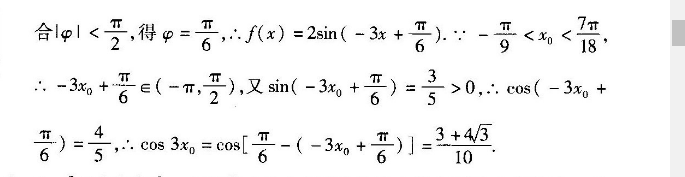
10.B【试题情境】本题是综合性题目,属于探索创新情境,具体是数学探究情境,以三角函数为载体考查正弦函数的图象与性质.【关键能力】本题考查逻辑思维能力、运算求解能力解题思路】先根据函数图象确定f(x)的最小正周期及a的可能取值,并通过最高点及题目给定的范围求φ及ω,进而得出∫(x)的解析式,然后借助∫(x)=5(-

1l.C【必备知识】本题考查的知识是“掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题【关键能力】本題考查逻辑思维能力,运算求解能力【学科素养】试题以平面四边形为载体考查解三角形的知识,需要考生利用正弦定理与余弦定理解三角形,考查数学探索学科素养【解题思路】解法一已知→设AB=4x,AD=3弦定理2余弦定理AD=6.b=8cos∠ABD5∠ABC=9→sin∠DBC=诱导公式5正弦定理解法二已知一→设AB=4x,AD=3x余弦定理→AB=8,AD=6分别延长BC,AD交于点EAE=16→DE=10∠ABC=90°,∠BAD=60°∠CDE=90°∠BCD=120°∠DCE=60°【解析】解法一因为3AB=4AD,所以可设AB=4x,AD=3x,在△ABD中,BD=2√13,∠BAD=60°,由余弦定理可得(213)2=(3x)2(4x)2-2×3xx4 xx cos60°,得x=2,故AD=6,AB=8,结合余弦定理得cos∠ABD=AB+BD2-AD 52×AB×BD2因为∠ABD+∠DBC=∠ABC=90°所以sin∠DBC=cos∠ABD所以在△BCD中,由正弦定理可得CD= BAsin∠DBC23213=132,故选Csin∠BCD√3解法二分别延长BC,AD交于点E.因为3AB=4D,所以可设AB=4x,AD=3x,在△ABD中,BD=2√13,∠BAD=60°,由余弦定理可得(2√13)2=(3x)2+(4x)2-2×3xx4xcos60°,得x=2,所以AB=8,1D=6.又∠ABC=90°,∠BAD=60°,所以AE=16,则DE=10.因为∠BCD=120°,所以∠DCE=60°,易知∠CDE=90°,所以CD=DE010n∠DCE=3=32,故选C

以上就是数学周报易学通人教a版2020－2021选修1－1答案，更多英语周报答案请关注本网站。