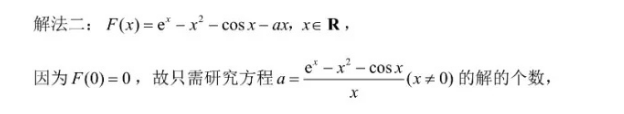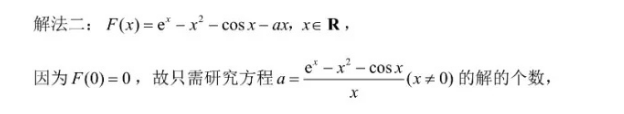6.若x23,则2+2,2=2222=4,必要性成立:当x=4y=22+2≥4成立,但是x=,充分性不成立,故选B


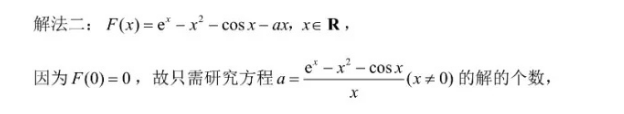


22.(本小题满分12分)解:(1)函数f(x)的定义域为R,求导得∫(x)=c2-a①当a≤0时,由f(x)>0恒成立,得f(x)在R上为增函数;②当a>0时,若∫(x)>0,则x>lna,若f(x)<0,则x
0时,f(x)在(-∞,lna)上为减函数,在(lna,+∞)上为增函数…………(5分)(2)解法一:F(x)=c2-x2-cosx-ax,x∈R,则F(x)=c2-2x+sinx-a,则F"(x)=c2+cosx-2,令g(x)CoS x则g(/se·sinx-e(2-cosx)sinx+cosr-2√22(e2)2所以g(x)在R上单调递减,又g(0)=1,故当x>0时,g(x)=
0当x<0时,。/_2-cosx>g(0)=1,即F"(x)=e'+cosx-2<0,又F"(0)=0,所以F(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,所以F(x)==F'(0)=1-a①当a≤1时,F(x)m=F(O)=1-a≥0,则F(x)在R上单调递增,由于F(0)=0,故此时F(x)在R上有且只有唯一零点②当a>1时,F(x)mn=F(O)=1-a<0,当x→+时,F(x)→+∞:当x→-∞时,F(x)→+∞,所以存在x<0
0>F(x2),又当x→+∞时,F(x)→+∞:当x→-时,F(x)→-∞故此时F(x)在R上有3个不同的零点,综上:当a≤1时,F(x)有且只有唯一零点:当a>1时,F(x)有3个不同的零点(12分)解法二:F(x)=e-x2-cosx-ax,x∈R因为F(0)=0,故只需研究方程a=-x-c03x(x≠0)的解的个数,令G(x)r- cos x求导得G(x)=x(e'-2x+sin x)-(e'-x'-cosx)(x-I)e+xsinx-xcos x令h(x)=(x-1)e+ sinx-x2+cosx,x∈R,ol h(x)=xe'+sin x + xcosx-2x-sin x= x(e+ cos x-2)令g(x)2-cosxx∈RRg(r)=e.sin.x-e(2-cos x)sIn xtinx+cos x-2所以g(x)在R上单调递减,又g(0)=1,故当x>0时,g(x)=2-0sx
0,则h(x>0当x<0时,g(x)=2-cosxc+>g(0)=1,即e+cosx-2<0,则h(x)>0,所以h(x)在R上单调递增,而h(O)=0,所以当x>0时,h(x)>0,即G(x)>0,即G(x)在(0,+∞)上单调递增;当x<0时,h(x)<0,即G(x)<0,即G(x)在(0,+∞)上单调递减,由洛必达法则知:imo(x)=mS-x2- cosx lim(c-2x+six)=1,.im G(r)= lim e'-r-cos x- lim(e'-2x+sinx)=+oolim G(x)= limlim(e-2x +sin x)=+oo,故当a>1时,方程a=G(x)在(∞,0)U(0,+∞)共两个不等根当a≤1时,方程a=G(x)在(-∞,0)∪(0,+∞)无实根又F(0)=0,综上:当a≤1时,F(x)有且只有唯一零点:当a>1时,F(x)有3个不同的零点……………(12分)

以上就是2022英语周报 KMD答案,更多英语周报答案请关注本网站。