2022英语周报8上答案

20.(1)证明:如图,延长AF,交BB1的延长线于点M,连接PM,由F是A1B1的中点,可得△AA1F≌△MB1F所以MB1=AA1=2,由题得B1P=2,故MB1=B1P,所以∠B1PM=45°,由题得EC1=PC1=1,所以∠C1PE=∠B1PM=45故E,P,M三点共线,因为直线EP与直线AF交于点M,所以A,E,P,F四点共面(6分)(2)解:连接B1Q,由题意得B1Q∥平面AEPF,所以B1Q∥EP,所以BQ=BB1=2,由题意得BC,BB1,BA两两垂直,则以B为原点,以BA,BB1,BC所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系则F(1,2,0),Q(0,0,2),P(0,2,2),E(0,1,3),故Q=(1,2,-2),@=(0,1,1),Q=(0,2,0)(9分)设n=(x1,y,x1)为平面EQF的法向量+2y1-2x则z1=0可取n=(4,-1,1)(10分)设m=(x2,y2,z2)为平面QFP的法向量,则QF=0,m/x+212-2x2=0可取即m=(2,0,1)(11分所以oos(n,m3√0n·m√6+1+1×√4又由图易知二面角PQFE为锐角,所以二面角PQFE的余弦值为3①0(12分)

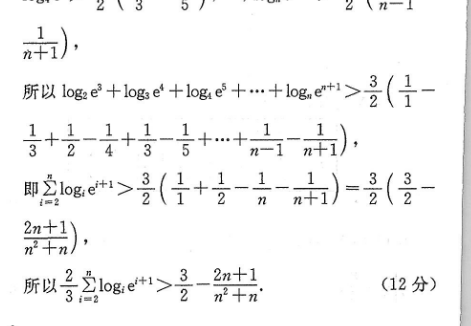
22.(1)解:由题意得x>0f(x)=3x-3d2=3(x2-a23(x-a)(x2+ax+a2)(1分)显然(x+号)+32>0(2分)当a≤0时,x-a>0,f(x)>0,所以f(x)在区间(0,十∞)内单调递增,无极值;(3分)当a>0时,x∈(0,a)时,f(x)<0;当x∈(a,+∞)时,f(x)>0所以f(x)在区间(0,a)内单调递减,在区间(a,+∞)内单调递增所以f(x)在x=a处取得极小值f(a)=a3-3a3lna1,无极大值(5分)(2)证明:由(1)可知,当a=1时,f(x)=x3-3lnx-1≥f(1)=0(6分)故当x>1时,x3-1>3lnx,又n>1,所以n3-1>3lnn,又n23-1=(n-1)(n2+n+1)<(n-1)(n2+2n+1)=(n2-1)(n+1),(8分)所以(n2-1)(n+1)>3lnn,故In nn2-1'即kge3=2(n2-n+1)(10分)故kge>2(1-3),kgs>2(2-1)a+1n+1n+所以ke+kge+ke+…+kge>2(3+2n-1n+1)即ge>2(1+2-1-n)=2(22n+1n2+n所以2∑1ge+172n2+n(12分)

以上就是2022英语周报8上答案，更多英语周报答案请关注本网站。