2022 英语周报 高一 XN 12答案

1l.ABD【解析】由于a>0,b>0,则“a>b”与“a2>b2”等价,故A正确;由>b21得mk>0.则m,则有呢21k2,.B正确:设函数∫(x)=、r(x)=1-,则∫(x)在(0,)单调递增,在(e,+∞)单调递减,设a>b>e,则有f(a)

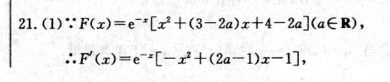
21.(1)∵F(x)=e[x2+(3-2a)x+4-2a](a∈R),∴F(x)=e-“[-x2+(2a-1)x-1],令h(x)=F(x),则h'(x)=e-*(x2-(2a+1)x+2a)=e-x(x-2a)(x-1),h(x)=0得x1=1,x2=2a∴当a>时,有x∈(-∞,1)时,h'(x)>0x∈(1,2a)时,h'(x)<0,x∈(2a,+∞)时,h(x)>0h(x)在(1,2a)上单调递减,在(-∞,1),(2a,+∞)上单调递增;当a=时,h(x)≥0在R上恒成立,于是h(x)在R上单调递增;当a<2时,x∈(-∞,2a)时,h(x)>0,x∈(2a,1)时,h'(x)<0,x∈(1,+∞)时,h'(x)>0,h(x)在(2a,1)上单调递减,在(-∞,2a),(1,+∞)上单调递增综上,当a>2或当a<2时,h(x)有两个极值;当a=2时,h(x)无极值.(6分)(2)解法一:f(x)>fx)+(2a+1)g(x)(x)-=(x)22+1,由(1)其中h(x)=(x)=f(x),:①当2a≤0,即a≤0时,由(1)可知,h(x)在[O,1)上单调递减,在[1,m]上单调递增当x∈[0,m]时,h(x)m=h(1),依题意有h(1)=e1(-1+2a-1-1)=2a-3z2a+1,解得a≤2=2,a≤2e=2②当0<2a<1,即0 0,2a≤二x=x-1-c,设t(x)e, E[O, m].则(a)-=21g2x-1-e)(e-1)(x2-1)(1+e)(e-x)易知1+e>0,∴当x∈(0,1)时,t'(x)<0,t(x)<0单调递减,当x∈(1,m)时,t(x)>0,t(x)<0单调递增,(x≥1)=31∴2a≤e31.as≤28=2故实数a的取值范围为(∞,2e-231.(12分)

以上就是2022 英语周报 高一 XN 12答案，更多英语周报答案请关注本网站。