九年级英语周报新目标2022-2022第20期答案

语篇解读:本文是一篇记叙文。三岁的奥罗拉有一天晚上走失,忠实的老狗Max一直陪伴在小主人身边,直到最后获。24.选A细节理解题。根据首段中的“ But Max was getting on in years, with his lack of hearing...”可知,Max因为年老而听力变差。故选A25,选B詞义猜测题。根据上下文可知,当奶奶看到岁的奥罗拉的时候激动得连哭带笑,而三岁的孩子对这是无法理解的,由此推断孩子会感到困惑。故选B26.选D细节理解題。根据第三段末句和第四段首句可加,当奥罗拉听到奶奶的喊声时做出了回应,这样她才被找到。故选D27.选C标题归蚋题。年仅三岁的奥罗拉走失的夜晚,老狗Max忠诚地陪伴着小主人,温暖着她,直到被人们找到。由此可知虽然固年老而听力变差,但MaxX还是证明了自己的价值。故选C。

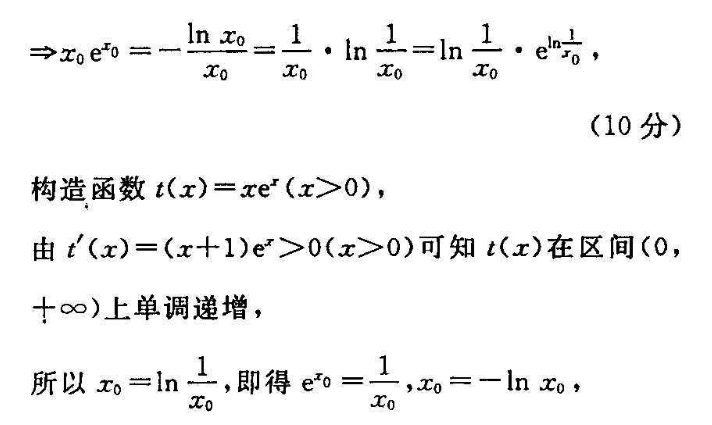
21.解:(1)f(x)的定义域为(0,+∞),所以f(x)=lnx+(a-1)x+1得f(x)=上+,‘1+(a-1)x(1分)当a≥时,(x)>0,函数r(x)在区间(0,+∞)上单调递增;(2分)当a<1时,记g(x)=1+(a-1)x,则函数g(x)=1+(a-1)x在区间(-∞,+∞)上单调递减,令g(x)=0→x所以当x∈(0,1)时,g(x)>0,即∫(x)>0,函数f(x)在区间(1)上单调递增;当x∈(12,+∞)时,g()<0,即f(x)<0,函数(2)在区间(12+∞)上单调递减综上所述可知:当a≥1时,函数f(x)在区间(0,+如)上单调递增;当a<1时,函数f(x)在区间(0上单调递增;在区间,+∞)上单调递减(5分)(2)不等式f(x)≤e恒成立等价于(a-1)x≤xenx-1恒成立,即a-1≤的-1x-1恒成立即a-1≤(6分)记x)=e-12-1(x>0),所以(x)=e-1-lnx11=fe+lnxie h(x)=x2e+In x, (x>0)易知函数h(x)在区间(0,+∞)上单调递增,又因为k(1)=6>0,1(1)=c2-1<0,所以存在x∈(,1),使得h(x0)=0,(8分且当x∈(0,x)时,h(x)<0,即g(x)<0,从而q(x)单调递减;当x∈(x0,+∞)时,h(x)>0,即g(x)>0,从而φp(x)单调递增,所以g(x)的最小值为g(x)=eo又因为由h(xo)=0,得xe+lnxo=0→xe=-型=1NCo10分构造函数t(x)=xe(x>0),由t(x)=(x+1)e>0(x>0)可知t(x)在区间(0,十∞)上单调递增,所以x=1nx,即得_1,o=-hnx0,所以g()=1+2-1=1;所以a-1≤1→a≤2,故实数a的取值范围为(-∞,2].·(12分)

以上就是九年级英语周报新目标2022-2022第20期答案，更多英语周报答案请关注本网站。