2022 英语周报 九年级 新目标（KMD） 8答案

17.解:(1)因为cos∠ACB=-17,∠ACB∈(0,4√3r),所以sin∠ACB=/177在△ABC中,由正弦定理得,bsinBin∠ACB所以b=- C Sin B143sin∠ACB314√3又b=14c0sB,所以3sinB=14cosB,所以tanB=√3,因为B∈(0,π),所以B=(2)由(1)可得b=14在△ACD中,cos∠ACD=-co∠ACB=-,由余弦定理可得:AD2=AC2+CD2-2ACCD·cos∠ACD,即(2√21)2=72+CD2-2×7×CD,即CD2-2·CD-35=0,解得CD=7或-5(舍去),所以CD=7

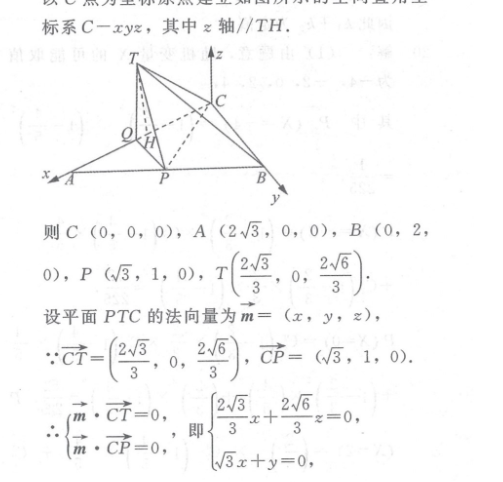
18.(1)证明:∵P,Q分别为AB,AC边上的中点,∴PQ/BC,PQ=2BC∵AC=2√3,BC=2,AB=4,∴AC2+BC2=AB2,∴AC⊥BC,则PQ⊥AC,故翻折后TQ⊥PQ,且PQ=1.PQ⊥AC,PQ⊥TQ,TQ∩AC=Q,∴PQ⊥平面TQC又BC//PQ,故BC⊥平面TQC,BCC平面ABC,故平面TQC⊥平面ABC(2)解:由(1)证知BC//PQ,∴异面直线PQ与BT所成的角即为∠TBC,故∠TBCBC⊥平面TQC,∴BC⊥TC,即△BTC为等腰直角三角形,∴TC=BC=2又由(1)所证知TQ=QC=3,PQ=2BC=1.在△TQC中过点T作TH⊥QC于点H平面TQC⊥平面ABC,平面TQC∩平面ABC=QC,故TH⊥平面ABC×2×√(3)2-12=√2.在△TQC中由等面积法可求得TH=2v6以C点为坐标原点建立如图所示的空间直角坐标系C-xyz,其中z轴//TH则C(0,0,0),A(2√3,0,0),B(0,2,0),P(3,1,0),y(23。2√6设平面PTC的法向量为m=(x,y,z),∵C个2√3√60,3),Cp=(3,1,0).=0,即/3+26m,C个=02√303x+y=0令z=1,可得m=(-2,√6,1)又平面TQC的法向量为n=(0,1,0),√6∴cos〈m,n)√3∴二面角P-TC-Q的正弦值为

以上就是2022 英语周报 九年级 新目标（KMD） 8答案，更多英语周报答案请关注本网站。