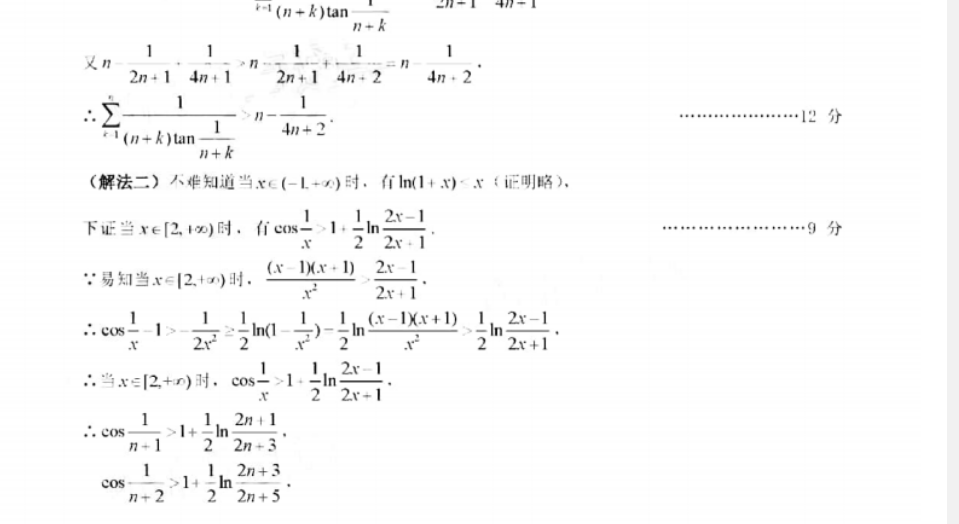
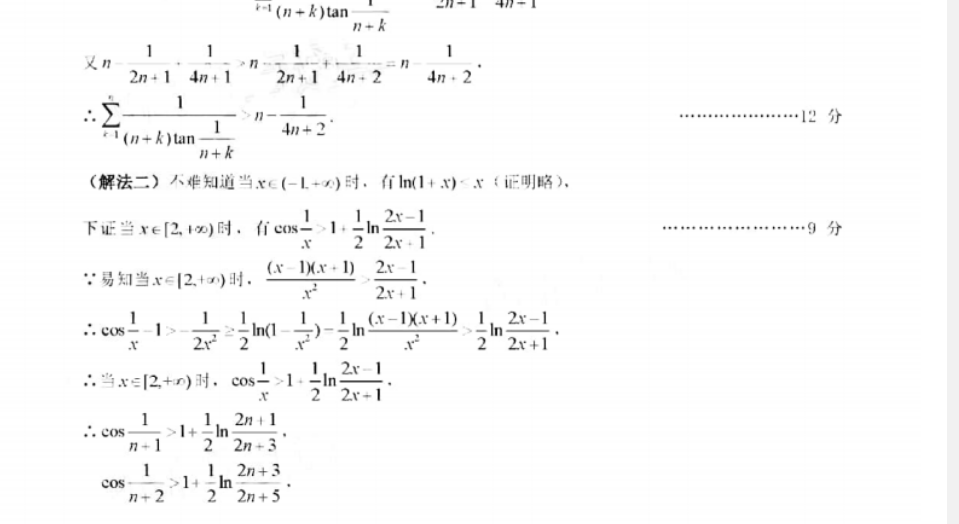

12分)已知定义在R上的函数f(x)=x+asx+(a-2)2,a∈R.(其中常数c是目然对数的底数,e71828..)(1)当a=2日,求f(x)的极值(2)(i)若f(x)在10.x上单週递坦,求实数a的取值范围:(i)当〃∈N时,证明:(n+k)tan4n+解:(1)当a=2时,f(x)-x-2cosxf(x)=2(r-sin x).令g(x)=x-sinx,则g(x)=1-cosx20∴g(x)在(-x、+∞)上单调递增,又g(0)=0,∴当x∈(x.0)时,g(x)
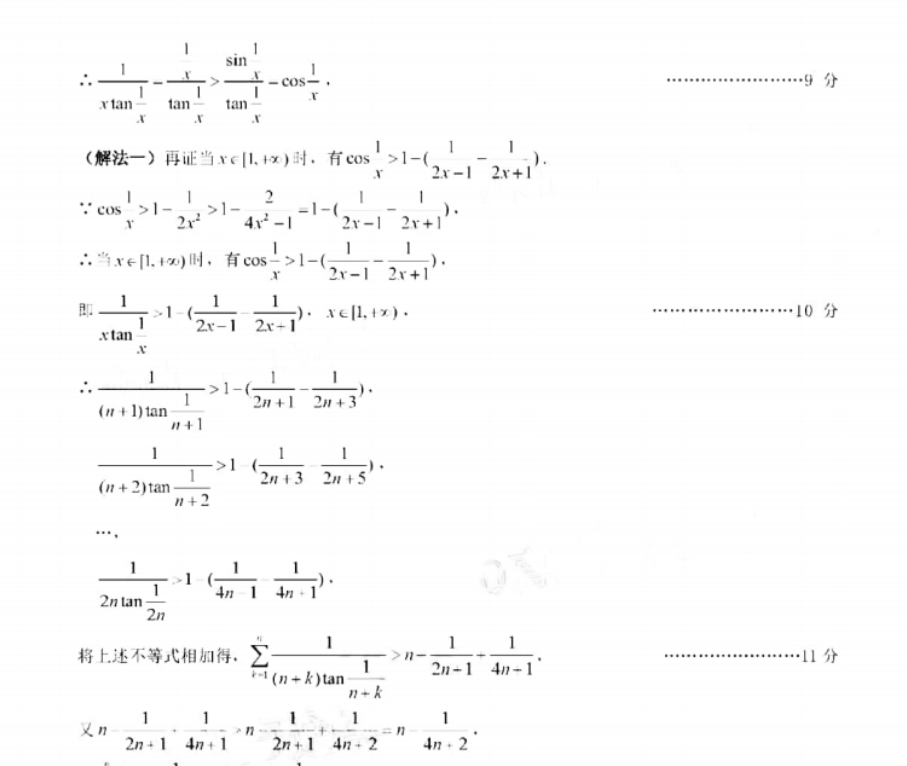
8(0)-0当x∈(0)时,f(x)<0:当x∈(0.4x)时,f(x)>0∴∫(x)在(,0)上单调递减;在(0.+x)上单灣递增∴f(x)的极小值为f(0)-2.尢极大值(2)(1)易知f(x)=2x- asIn-(a-2)若f(x)在[.x1.单调递增,以.2x- asin r-(a-2>0(*)在10.x】上恒成立(解法一)显然当x∈10.r时sint+e>0不等式(*)等价a2(x·c)…4分sin.\+ e下Ee> 1. re[0. Isina-tB证x+c'sinx+c"xcl0.xx-sinx20,x=[0.x],由(1)可知,星然成立,0.xsina+e或者考虑x=sx21可(由(1)可知x-sinx≥0,xc10x).……分sint esin t I e又当x-0时,sint e∴a≤2,田实数a的取值范围为(x.2……7分(解法)不等式(非)在10.x上但成立对于Vx,c10.m,均育-(sinx-c“ka-2(x+c“)≥0当a∈(2.+∞)时,令x=0,上述不等式旱然不成立…45分2当a∈(-x,2]时,令Ma)--(sint-c“h-2(x-c“)易知爪(a)在(-∞,+∞)上单调递减,∴当a∈(-x2]时,h(a)≥h(2)=2(x-sinx)……………6分主(1)可知,当xc10.x时,x-sinx20.∴ha)≥0∴当ae(x2]时,Vxcl0.x,均有sinc-c“+2(5-c“)20综上所述,当且仅当a(一x,2时,不等式(*)在10x上恒成立,却使得f(x)在10.x上单调递增的实数a的取值范为(-x,2]…分(i)先证当xc(0.1]时,有cosx>l(解法一)由(1)可知.当a=2时,f(x)=x2-2cosx在0.x上单调递∴当xc(0.1时,f(x)>f(0),cosx>1解法一)由(1)可知,当xc(.时,r>sinx>0∴x>sin-x,x∈(0.∴当x∈(0.11时,cosx=1-2sin(=)1-2(=)=1cos x>1……………8分∴当x(0.时,有∞sx>1-当x∈l+)时,易知1≥0∴COS-9分rlan- tan- tan(解法一)再证当x1+x)时,有cos>1-nx-12x+∵cos>l2x24x22x-12x+∴当xn,)时,有c01-(2x-1-2x+)ttan(n t l)tanl2H+3(n +2)tan>1(2n432n5将上述不等式相加得11分1(n+k)tan2n+14n+12n+14n+24n21(n+k)tan2n+14n+12n+14(n+k)tan(解法二)人难知道当x∈(-1+)时,fhn(1+x)x(证明略),下证当x∈[21∞)时,fcs-1=ln2r:1∵易知当x=|2.+)时(x-1x+1)2:-1: coShn(--)--ln(x-1Xx+1),2x-122t+1∴当x=2+n)时,cos-1-;h22x+1+12n+31+-n2n+5cos>1+-In将上述不等式相加得2n+1CoS分,coyl+..+ cosIn(210分下uhn(2-x)
b3、1下il÷->0,即证e551王证c(5y-125.5然成立又当n∈N时∈(0,-]2n+1In(2COS月+24n+2e(n+k)tan月+k【合题意图】本题以基本初等函数的极憤、单澜性河题和不等式证明为毂体,考学生利用导数分析、解祆门题的能力,分类讨论、化归转化想想和昱釦推理、数学运算等核心素养,具有较强的综合性

26.(14分)(1)16Fe+8H2O+ Cures.2=Cu2+17Fe2+2S04+16H'(2分)加热(2)2MoS2+7022MoO3+4S02(2分)(3)酸性(2分)(4)1.0;(1分)60min;(1分)作氮肥(作炸药等)(1分)高温(5)H, Mo0, Li2 CO3Li2MoO4+CO2↑+H20(2分);C(1分)(6)3.3≤pH<4.5(2分)

以上就是2021-2022 英语周报 九年级 新目标 11五版答案,更多英语周报答案请关注本网站。