2021-2022英语周报初一第三期答案

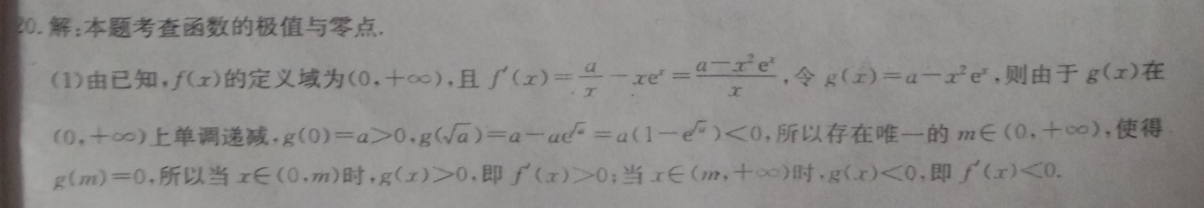
解:本题考查函数的极值与零点(1)由已知,f(x)的定义域为(0,+∞),且(x)=一x=C,令g(x)=a-xe,则由于g(x)在(0,+∞)上单调递减,g(0)=a>0,g(a)=a-ac=a(1-)<0,所以存在唯一的m∈(0,+c),使得g(m)=0,所以当x∈(0,m)时,g(x)>0.即f(x)>0;当x∈(m,+∞)时,g(x)<0,即f(x)<0所以f(x)在(0,+∞)上有唯一极值点(2)因为f(2)>e(-e+h2),所以a>e①由(1)知f(x)令g(x)=a-x2e,由a>e得g(1)=a-e>0,所以g(x)=0在(1,+∞)内有唯一解,从而f(x)=0在(1,+∞)内有唯一解x0,则f(x)在(1,x)上单调递增,在(x,+∞)上单调递减,所以x0是f(x)的唯一极值点令h(x)=hnx-x+1,则当x>1时,h(x)=x-1<0,故h(x)在(1,+∞)内单调递减,从而当x>1时h(x) e,lna>1时,有f(lna)=aln(lna)-(lna-1)em 1时,nx

21.(12分)解:(1)由f(x)=x(1+a+ a cos d),得f(x)=1+a+ u cos a- a sin T,分所以f(x)=r,…………………………………2分3分所以曲线y=f(x)在点(r,f(x)处的切线方程为y-r=x-π,即y=x4分(2)当a=1时,f(x)=x(2+cosx),则f(x)≥ sIn等价于x(2+cosx)≥ nisIn ..当x∈0,时,x(2+cosx)≥0,sinx≥0,5分当m≤0时,f(x)≥ nsIn.T恒成立;6分当m>0,x∈0,时,x(2+cosx)≥ sin , t恒成立等价于-。出≥0COS 7sIn.71+2cos 3gm 2+cos r则g(x)m(2+cosx)2’…………,,,…………7分设t=cosx,则t∈[0,1],h(x)=1+2,(t)==2(+2)(=1)==2(=1)≥0,+t所以h(t)在[0,1]上递增,所以h()的值域为438分①当≥言即0

以上就是2021-2022英语周报初一第三期答案，更多英语周报答案请关注本网站。