21年英语周报九年级第20期答案

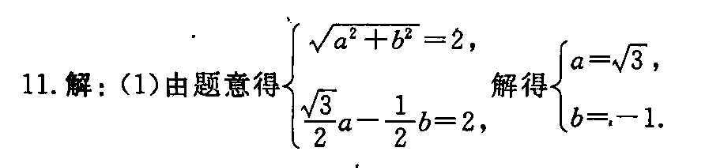
a=√3,11.解:(1)由题意得a2+b=2、b2b=2所以:x)=√3sing-cosx又因为(2)=2n(x一5)∈[2x],所以当x=π时,f(x)取得最小值是1(8分)(2)法一:由题得asin2x- SIn cos+a>0对x∈(o2)恒成立,dU a(1-cos 2x)-sin 2x+2a>0,即3a>sin2x+acos2x恒成立,所以3a>√a2+1,解得a>y2,故实数a的取值范圈是(,+∞)(20分)法二:利用分离变量法可得,只要a>2恒成立,即求y=5m2x+1的最大值tan因为y=sm2x+1=2m2x+c03x=2an2x+1,令nx=t(t>0),t+y=22+12t+-利用单调性易得函数u=2+的最小值为2√2,则1≤=y,所以2+12√2故实数a的取值范圄是(2,+∞(20分)

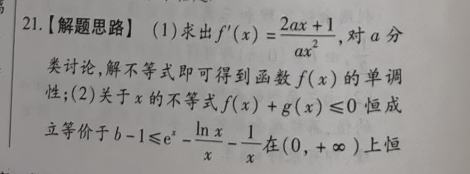
21.【解题思路】(1)求出f∫(x)=2ax+1,对a分x类讨论,解不等式即可得到函数f(x)的单调性;(2)关于x的不等式f(x)+g(x)≤0恒成立等价于b-1≤e2hnx)在(0,+∞)上恒成立,构建函数A(x)=c-1x-1,研究其单调性与最值即可【解析】(1)由f(x)=2mx-1+1得(x)=2+1=2mx+1(x>0),(1分)当a>0时、f(x)>0,则f(x)在(0,+∞)上单调递增(2分)当a<0时,由f(x)>0,得x>-;由f(x)<0,得0 0时、f(x)在(0,+∞)上单调递增;当a<0时,(x)在(0,-1)上单调递减,在1+∞)上单调递增(4分)(2)由题意知当a=-1时,要证不等式f(x)+g(x)≤0恒成立,即证2nx+x-1+(b(2)由题意知当a=-1时,要证不等式f(x)+g(x)≤0恒成立,即证2nx11+(b-1)x-xe-1-1mx+2≤0恒成立,即证b-1≤e2In x 1在(0,+∞)上恒成立(5分)令h(x)=eIn x8则(x)=-1212x+2=x令u(x)=x2e+hnx,则u(x)=(x2+2x)e+x>0,u(x)在(0,+∞)上单调递增,1、√e又u(1)=e>0,u()n2<04a(x)有唯一零点x( 0,即h'(x)>0,h(x)在(x0,+∞)上单调递增,h(x0)为h(x)在定义域内的最小值(9分)令k(x)=x(25x<1),则方程(※)等价于k(x0)=k(-lnxo),又易知k(x)在(,1)上单调递增,x0=-lnx,e=-,(10分)h(x)的最小值h(x0)=e°1=1.(11分)∵b≤2,b-1≤1=h(x0)≤h(x)恒成立,即关于x的不等式f(x)+g(x)≤0恒成立.(12分)【点睛】利用导数研究不等式恒成立或存在性问题,一般要构造函数,利用导数研究新构造函数的单调性,进而转化为最值问题求解

以上就是21年英语周报九年级第20期答案，更多英语周报答案请关注本网站。