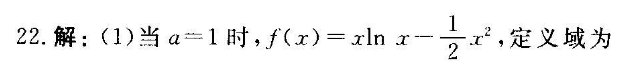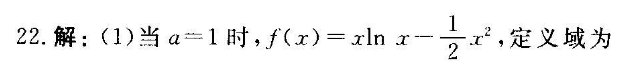




2解:(1)当a=1时,f(x)=xx-x2,定义域为(0,+
0当x∈(1,+∞)时,g(x)<0所以函数g(x)在区间(0,1)上单调递增,在区间(1十)上单调递减,g(x)的最大值为g(1)=0,所以当x>0时,g(x)≤0,即f(x)≤0所以函数f(x)在区间(0,+∞)土单调递减.(4分)(2)已知得g(x)=xlnx-ax2+(a-1)x则g'(x)=ln记h(x)=lnx-ax+a,则h(1)=0,h(x)=1-a=1-ax分①若a≤0,则当x∈(0,+∞)时h(x)>0,h(x)在区间(0,+∞3)上单调递增,且当x∈(0,1)时,h(x)
h(1)=0,即g(x)>0又g(1)=h(1)=0,所以函数g(x)在x=1处取得极小值,满足题意.(7分)②若0
1,当x∈(o,0)时+,h(x故函数n(x)在区间(o.)上单调递增且当x∈(0,1)时,h(x)
(1)=0,即g(x)>0又g(1)=h(1)=0,所以函数g(x)在x=1处取得极小值,满足题意(9分③若a=1,则g(x)=f(x),由(1)知函数f(x)在区间(0,+∞)上单调递减故g(x)在区间(0,+c)上单调递减,不满足题意(10分)④若a>1,则0<1<1,当x∈(1,+∞)时,(1)<0,故函数(x)在区间(,+∞)上单调递减且当x∈(11)时,h(x)>h()=0,即g2(x)>0当x∈(1,+∞)时,h(x)


0.解:(1)设A(x1,y1),B(x2,y2),弦AB中点的纵坐标为a则y=8x1,y2两式相减得(y1+y2)(y1-y2)=8(x1-x2),由直线l的斜率为1,可知x1≠x2,所以2akA=2a=8,得a=4,即弦AB中点的纵坐标为4(5分)(2)由题知,直线的斜率不为0.设直线AB:x=my+n,代入y2=8x,得y-8my△=64m2+32n>0,①y+y2=8m,yy2=-8n,②(7分)因为(AF-OF)·(FB+OF)=AO·OB=0因为(AFOF)·(FB+OF)=AO·OB=0,所以x1x2+yy2=0,即·+88+yy2=0,所以yy2=-64,n=8(10分)所以S△0MB=方×8×1y-y21=4(1y11+1y21)≥4×2√yy2T=64,当且仅当|y1=1y2|=8时取等号,所以△OAB的面积的最小值为6412分)

以上就是2022英语周报高二课标英语下学期阶段检测答案,更多英语周报答案请关注本网站。