2022-2022数学周报（12）九年级答案

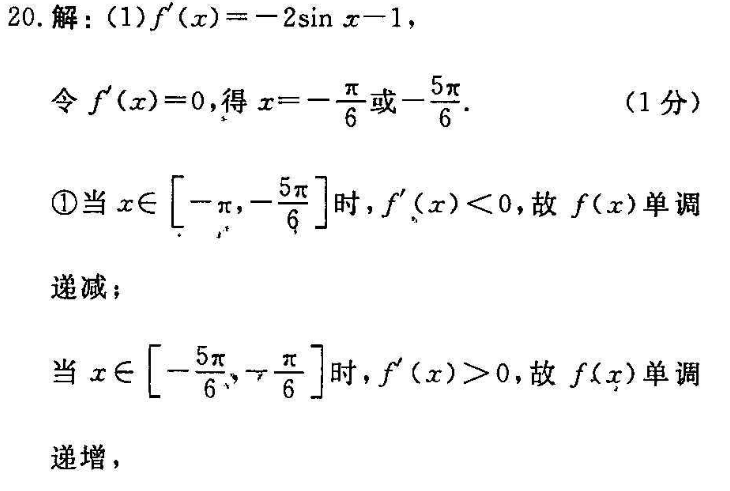
20.解:(1)f(x)=-2sinx-1,令f(x)=0,得x=-或5:6(1分)①当x∈L-,]时,f(x)<0,故f(x)单调递减;5当x∈一、—时,f(x)>0,故fx)单调递增,且f(-5)=5-3>0所以∫(x)在区间一x,-x上没有零点,(3分)②当x∈一,x时,f(x)<0,故f(x)单调递减,又f(-)=+>0,(m)=-2-n<0,f()f(π)<0.所以函数∫(x)在-x,x上存在唯一的零点综上所述,f(x)在[一,]上存在唯一的零点(6分)(2)若存在x∈(0,2),使得不等式f(x)+az>2成立,即存在x∈(0,),使20+ax-x-2>0成立& g(r)=f(r)+ar-2=2cos rtar-x-2,则g(0)=0,g(x)=a-1-2sinx,当x∈(0,2)时,1+2nx∈(1,3,所以g(x)∈(a-3,a-1),由于a-1≤0,即a≤1时,g(x)<0,g(x)单调递减,g(x) 0,即a>1,此时g(0)=a-1>0,因为g(x)=a-1-2sinx在(0,)上单调递减,当a-3≥0时,g(x)>0,所以g(在(O)上单调递增,g(x)>g(0)=0,即f(x)2ax>2;(10分)当a-3<0时,总存在t∈(o,2)使得(D=0,所以存在区间(0,t),使x∈(0,t)时,g(x)>0,所以g(x)在(0,t)上单调递增,则当x∈(0,t)时,g(x)>g(0)=0,即f(x)+ax所以实数a的取值范围是(1,+∞)(12分)

15.1m+k-1【解析】因为斐波那契数列{an}满足a=1,a2=1,a,=am-1+am-2,,a3=an+a2;a4=a2+a3=an+a2+1;a5=a3+a4=a1+a2+a3+1;a+2=a+1+an=a1+a2+a3+…+an+1=S+1;故an+2-Sn=1(n≥1,n∈N)所以S208=am20-1=m-1,因为a1+a3+a3+…+a2m9=a1+a1+a2+a3+a4+…+a20+aml=a1+S208=1+m-1=ma2+a4+a6+…+aa=a2+a2+a+a4+as+…+aalg+a29=S20l=aa1-1=k-1,故a1+a2+a3+…+am=m+k-1(第一空2分,第二空3分)

以上就是2022-2022数学周报（12）九年级答案，更多英语周报答案请关注本网站。