2020－2022数学周报第14期答案

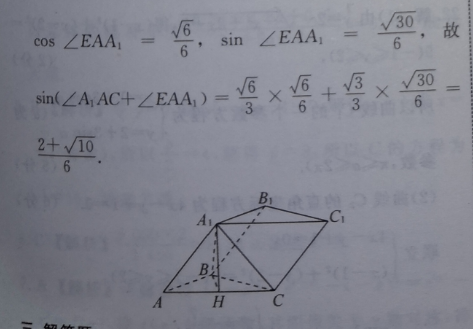
16.2+、①【解析】如图,在三棱柱ABCA1BC中,取AC的中点H,连接A1B,BH,A1H,A1C,设三棱柱的高为h,则S△ABC×h×2×2×h=4,解得h=2.在√3△AC中,由tan∠A1AC=√2得cos∠AAC=3sin∠A1AC=3由余弦定理知A1C=AA+AC√32AA1·AC=6,故△AA1C为等腰三角形,故3A1H⊥AC,且A1H=2,因此A1H⊥平面ABC.在Rt△A1BH中,BH=√2,A1H=2,故A1B=√6.又4+6-6AA1=√6,AB=2,故cos∠BAA1=2×2×√66,故√6cos∠EAA16,sn∠EAA1故cos∠EAA1=sin∠EAA故66sn(∠AC+∠EA4)=26×6+3×3062+√10BIC

12.C【解析】作出函数f(x)的部分图像如图所示,f(x)]2+a=(a+1)f(x)可化为[f(x)-1]·[f(x)a]=0,若方程[f(x)]2+a=(a+1)f(x)有5个根,由图可知f(x)=1有2个根,则f(x)-a=0应恰有3个根故实数a的取值范围为(0,1).故选C项=

以上就是2020－2022数学周报第14期答案，更多英语周报答案请关注本网站。