英语周报第八期八年级上册2022-2022答案

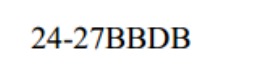
24-27BBDB

19.解:(1)∵四棱柱ABCD-A1B1C1D1是直四棱柱AB∥CD,在A1D1上取点M,连接EM,AM,EB,使得EM∥A1B1,则EM∥AB,且A1M=3A1D1,在矩形ADD1A1中,tan∠AHD=2,tan∠A1AMDH⊥AM,又DH⊥AB∵AB∩AM=A,AB,AMC平面ABEM,(4分)DH⊥平面ABEM,∵EFC平面ABEM∴DH⊥EF(6分)(2)∵四棱柱ABCD-A1B1C1D1为直四棱柱,∴AB⊥AA1又∵AB⊥DH,AA1∩DH=H,且AA1,DHC平面AA1D1D(2)∵四棱柱ABCD-A1B1C1D1为直四棱柱,∴AB⊥AA1又∵AB⊥DH,AA1∩DH=H,且AA1,DHC平面AA1D1D∴AB⊥平面AA1D1D,∴AB⊥AD,∴AB,AD,AA1两两垂直,所以以A为坐标原点,以AB,AD,AA1所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系,F设AF=a(0≤a≤5),则F(a,0,0),D(0,6,0),E(4,DE=(4,-4,4),∴DF=(a,-6,0)(8分)设平面DEF的法向量m=(x,y,z),E4x-4y+4z=0则所以令x=6,得平面DEF的一个法向量m=(6,a,a取平面AA1D1D的一个法向量n=(1,0,0),(10分所以|cos(m,n)2(a-3)2+543时,inm,n)=y3因此AF=3时,平面DEF与平面AA1D1D所成的面角的正弦值最小,最小值为(12分)

以上就是英语周报第八期八年级上册2022-2022答案，更多英语周报答案请关注本网站。