2022英语周报第30答案

21.解:(I)由函数f(x)是偶函数,得f(-x)=f(x),即mex-(-x)2+3=me-x2+3对于任意实数x都成立,所以m=0,2分此时h(x)=xf(x)=-x3+3x,则h(x3x2+3由h(x)=0,解得x=±1分当x变化时,h(x)与h(x)的变化情况如表所示(-1,1)(1,+∞)h(x)h(x)极小值极大值所以h(x)在(一∞,-1),(1,十∞)上单调递减,在(-1,1)上单调递增,所以h(x)有极小值h(-1)=-2,有极大值h(1)=分Ⅱ)由f(x)=me-x2+3=0,得m分所以“f(x)在区间[-2,4上有两个零点”等价于“直线y=m与曲线g(x)=x=3,x∈[-2,4有且只有两个公共点”对函数g(x)求导,得g(x)由g(x)=0,解得x18分当x变化时,g(x)与g'(x)的变化情况如表所示当x变化时,g(x)与g'(x)的变化情况如表所示(-1,3)(3,4)(x)0g(x)极小值极大值所以g(x)在(-2,-1),(3,4)上单调递减,在(-1,3)上单调递增.分又因为g(-2)=e2,g(-1)=-2e,g(3)=,g(4)所以g(3) g(-1),所以当一2cm<13或m=5时,直线y=m与曲线g(x)=x=3,x∈[-2,4有且只有两个公共点,即当一2e

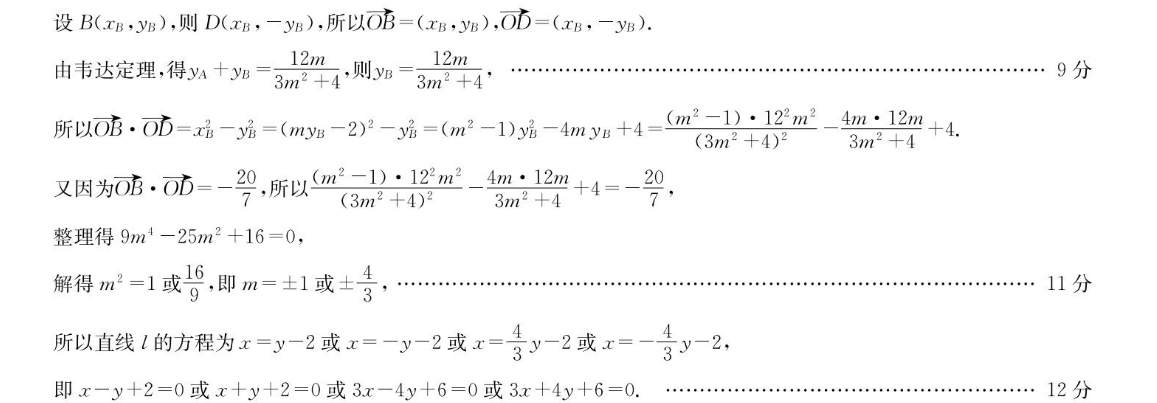
20.解:(I)由题意,得a=2,则PF1|+PF2|=2a=41分又|PF2|-1PF1=1,所以PF2=2,|PF1=2由题意,得c2=a2-b2=4-3=1,所以c=1,则F1F2|=2c=23分所以c∠FPF=PF已PF,FE上=3,则sm∠FPF=4,所以S△F1F2=2PF1|·|PF2|·sin∠F1PF,=3…5分(Ⅱ)由题意,得A(-2,0)当斜率为0时,明显不合理6分当直线斜率不为0时,设直线l为x=my-2.7分联立x21x2=1得(3m2+4)y2-12my=0由4=(-12m)2>0,得m≠08分设B(xB,y),则D(xB,-yB),所以OB=(xB,y),OD=(xB,-yB由韦达定理,得yA+yB12m-,则yB=3m2+4,…12m3m2+4分所以O·O5=x-y=(my1-2)2-=(m2-1)y-4my+4=m112m一切m:1m+4.又因为OB·Ob所以1)·1224m·124整理得9m4-25m2+16=0,解得m2=1或9,即m=±1或士3,…11分所以直线的方程为x=y-2或x=-y-2或x=3y-2或x=-3y-2,即x-y+2=0或x+y+2=0或3x-4y+6=0或3x+4y+6=012分

以上就是2022英语周报第30答案，更多英语周报答案请关注本网站。