2022英语周报高考52答案

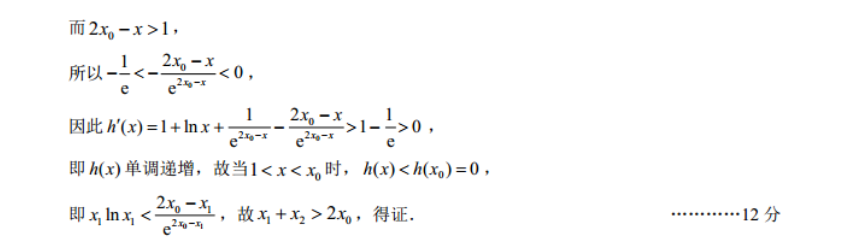
21.(12分)解:(1)g(x)的定义域为(0,+∞),g(x)1分当a≤0时,g'(x)>0恒成立,所以,g(x)在(0,+∞)上单调递增当a>0时,令g(x)=0,得到所以当x∈(0,-)时,g'(x)>0,g(x)单调递增,当x∈(-,+∞)时,g'(x)<0,g(x)单调递减综上所述当a≤0时,g(x)在(0,+∞)上单调递增当a>0时,g(x)在(0,-)上单调递增,在(-,+∞)上单调递减3分(2)F(x)=lnx--,定义域为x∈(0,+∞),F(x)=11而x∈(1,2),故F(x)>0,即F(x)在区间(1,2)内单调递增,又F(1)0,F(2)=ln2->0且F(x)在区间(,2)内的图像连续不断,故根据零点存在性定理,有F(x)在区间(,2)内有且仅有唯一零点5分所以存在x∈(2),使得F(x1)=0,即加≈、1且当1 x时,f(x)>=(x)>x,xhnx,1 0得m(x)单调递增:当x>x时,m(x)=由m'(x)<0得m(x)单调递减若m(x)=n在区间(1,+∞)内有两个不相等的实数根x,x2(x1 2x,即证x2>2x-x,又2x。-x1>x,而m(x)在区间(xa,+∞)内单调递减,故可证m(x2) 0当t∈(l,+∞)时,φ()<0,故o(n而()>0,故0<()<-,2x0-x>1,所以-1<-25-x12因此h(x)=102x一x即A(x)单调递增,故当1 2x,得证…12分

19.B〖解析】材料所给时间为1840年可知,工业资产阶级于1832年获得政治权力,为了刺激出口,减少印度棉织品对自身产品的冲击,对殖民地实施不平等的关税政策,从而保护英国的工业资产阶级的利益,B项正确。材料侧重英国利用关税政策控制英印贸易,而自由主义强调国家尽量减少对经济的干预,两者相冲突,排除A项;世界市场在此时已初步形成,排除C项;据材料“1814年印度向英国输出棉布品127万码,21年后缩减了3/4以上”可知,印度的工业化受到阻碍,排除D项。

以上就是2022英语周报高考52答案，更多英语周报答案请关注本网站。