2022英语周报高二38期答案

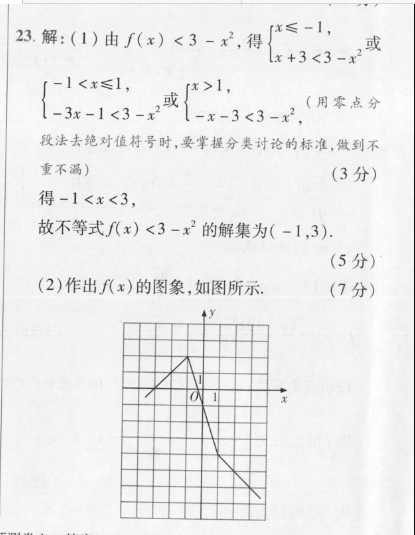
23.解:(1)由f(x)<3≤-1,得或+3<31 1,或1-x-3<3-x2(用零点分段法去绝对值符号时,要掌握分类讨论的标准,做到不重不漏)(3分)得-1

21.【试题情境】本题是综合性題目,属于课程学习情境和探索创新情境,具体是数学运算学习情境和数学探究情境品维导图】()1=0(x)=f'(x)=设切点坐标为(x0,-)(x-1)e→l的方程为点(0,0)在l上e°No(x0-1)→的方程为e2x-4y=0xo(2)(x)+e2≥0恒成立一等价转化f(x)mn≥-e对f(x)求导(x)=2-1构造函数g(x)、e-a,x>0(x-1)e求导g(x)≥g(1)=e-aa≤eg(x)≥0一f(x)的单调性一(x)m>a >eg(1)<0-(x)的单调性一f(x)m→a的范围→a的取值范围解:(1)当a=0时、f(x)f(x)=(x-1)e(1分)x设切点坐标为(x0,),(注意:点(0,0)不是切点)则l的方程为y(x-x)xo(2分)因为l经过点(0,0),所以得x0=2,所以l的方程为e2x-4y=0.(4分)(2)解法一f(x)+e2=0恒成立等价于f(x)≥e2.(点拨:将不等式恒成立问题转化为最值问题)(x)=(x-1)e,a(1-x)令g(x)=x-a,x>0,则g(x)s(x-1)e易知当x∈(0,1)时,g'(x)<0,g(x)单调递减当x∈(1,+∞)时,g'(x)>0,g(x)单调递增所以g(x)≥g(1)=e-a(6分)①当a≤e时,g(x)≥0所以当x∈(0,1)时,(x)<0,f(x)单调递减;当x∈(1,+∞)时,f"(x)>0、f(x)单调递增所以f(x)m=f(1)=e-a≥0>-e2,(7分)②当a>e时,g(1)=e-a<0,g()=a(e1)>0,所以存在x∈(0,1),使得g(x1)=0.(零点存在定理的应用)(a)=a(2-1),设g(a)=eLa>e则et(a)=(a-=2)°>0,所以g(a)0,即g(a)>0,所以存在x2∈(1,+∞),使得g(x2)=0,所以当x∈(0,x1)和x∈(1,x2)时,f(x)<0,f(x)单调递减;当x∈(x1,1)和x∈(x2,+∞)时,f(x)>0f(x)单调递增,(点:不要忽略对的符号的判所以f(x)=minf(x)f(x2)}.(10分)因为=a,i=1,2,所以x1-mnx;=lna所以(x)=+a(lmx-x)=a-ama所以f(x)mn=a(11分)设k(a)=a-alna+e,a>e,则k(a)=-lna<0所以k(a)在(e,+∞)上单调递减,在忌封e)=U,所以e 0,则x-lnx=lna所以f(x)=t-aln.因为g'(x)=(x-1)°,所以当x∈(0,1)时,g(x)<0,g(x)单调递减;当x∈(1,+∞)时,g'(x)>0,g(x)单调递增所以g(x)≥g(1)=e所以f(x)+e2≥0在x∈(0,+∞)上恒成立等价于1-alnt+e2≥0在te[e,+∞)上恒成立(8分)设F(t)=t-alnt+e2,t≥e,则F"(t)=若a≤e,则F"(t)≥0,F(t)单调递增F(1)=n=F(e)=e-a+e2>0若a>e,当t∈(e,a)时,F"(t)<0,F(t)单调递减;当t∈(a,+∞)时,F"(t)>0,F(t)单调递增则F(t)mn=F(a)=a-alna+e2≥0.(10分)设φ(a)=a-alna+e2,a>e则g'(a)=-lna<0所以φ(a)在(e,+∞)上单调递减,注意到(e2)=0,所以e

以上就是2022英语周报高二38期答案，更多英语周报答案请关注本网站。