2022英语周报 高二 课标综合答案

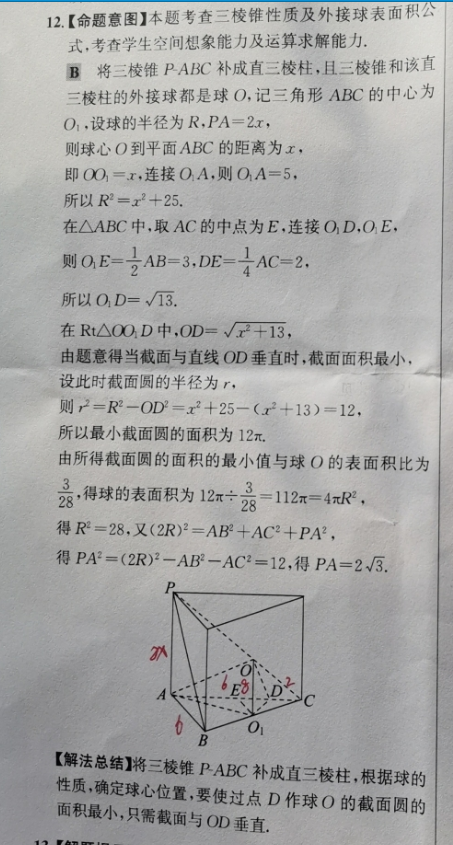
12.【命题意图】本题考查三棱锥性质及外接球表面积公式,考查学生空间想象能力及运算求解能力B将三棱锥PABC补成直三棱柱,且三棱锥和该直三棱柱的外接球都是球O,记三角形ABC的中心为O1,设球的半径为R,PA=2x,则球心O到平面ABC的距离为x即OO=x,连接OA,则OA=5,所以R2=x2+25在△ABC中,取AC的中点为E,连接OD,O则OF21B=3,DE=AC=2所以OD=√13在Rt△OOD中,OD=√x2+13,由题意得当截面与直线OD垂直时,截面面积最小设此时截面圆的半径为r,则r2=R2-OD2=x2+25-(x2+13)=12所以最小截面圆的面积为12兀由所得截面圆的面积的最小值与球O的表面积比为28,得球的表面积为12x÷23=12x=4R2,得R2=28,又(2R)2=AB2+AC2+PA2,得PA2=(2R)2-AB2-AC2=12,得PA=2√3ACO【解法总结】将三棱锥PABC补成直三棱柱,根据球的性质确定球心位置,要使过点D作球O的截面圆的面积最小,只需截面与OD垂直

1.【命题意图】本题考查平面向量数量积和模的运算Ccos(b, c)Tb.c 12a+b12+b12+b24b2(2a+b)b(60+b)得b|=25,所以{a+b|=√(a+b)2=√9+12+20=√41.

以上就是2022英语周报 高二 课标综合答案，更多英语周报答案请关注本网站。