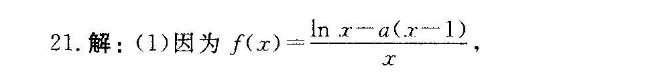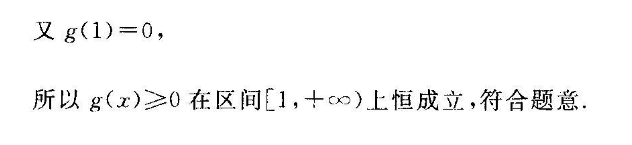19.解:(1)函数f(x)的图象经过点A(0,2),B(1,3),+lb=2所以即a+b=3,"b=1,所以f(x)=2+1.(3分)因为2x>0,2x+1>1,即f(x)>1,所以y=f(x)∈(0,1)故y=x2的值域为(0,1(6分(2)当a>1时,函数f(x)=a2+b在[-1,0]上为增函数,a-1+b=-1,由题意得无解(8分)a0+b=0,当0
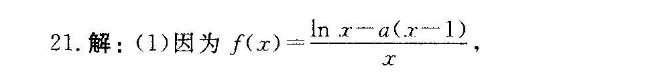


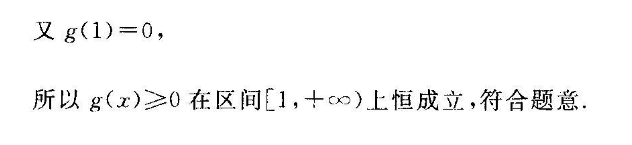

21.解:(1)因为f(x)In x-a(2-1)所以函数f(x)的定义域为(0,+∞),且f(r)(2分)令f(x)>0得lnx<1解得0
1-a,解得x>e-a所以函数f(x)的单调递增区间为(0,c1“),单调递减区间为(el-,+∞)(5分)(2)当x≥1时,1-xf(x)≤e-等价于e-1+lnx& g(x)=e+In x-ar+a-1=e+In x-a.x+则g(x)=e-1+1-a,(7分设h(x)=g(x),则h(x)=et8分)因为当x≥1时,h(x)>0所以h(x)在区间[1,+∞)上单调递增,即g'(x)在区间[1,+∞)上单调递增因此,g'(x)mn=g'(1)=2-a,(9分)当a≤2时,g(1)≥0,g(x)≥0在区间[1,+∞)上恒成立,所以g(x)在区间[1,+∞)上单调递增.又g(1)=0所以g(x)≥0在区间[1,+c)上恒成立,符合题意当a>2时,g(1)<0,存在x∈(1,+∞),使得当x∈(1,x)时,g(x)<0,从而g(x)在区间[1,x。1上单调递减,又因为g(1)=0所以当r∈(1.xn)时,g(x)<0,不合题意综上,a的取值范围为(-cx,2](12分)

以上就是2022 英语周报 高三 牛津 5答案,更多英语周报答案请关注本网站。