20192022英语周报高一35期答案

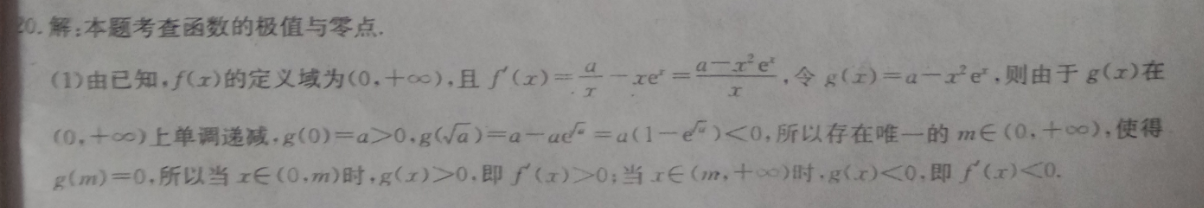
解:本题考查函数的极值与零点(1)由已知,f(x)的定义域为(0,+∞),且(x)=一x=C,令g(x)=a-xe,则由于g(x)在(0,+∞)上单调递减,g(0)=a>0,g(a)=a-ac=a(1-)<0,所以存在唯一的m∈(0,+c),使得g(m)=0,所以当x∈(0,m)时,g(x)>0.即f(x)>0;当x∈(m,+∞)时,g(x)<0,即f(x)<0所以f(x)在(0,+∞)上有唯一极值点(2)因为f(2)>e(-e+h2),所以a>e①由(1)知f(x)令g(x)=a-x2e,由a>e得g(1)=a-e>0,所以g(x)=0在(1,+∞)内有唯一解,从而f(x)=0在(1,+∞)内有唯一解x0,则f(x)在(1,x)上单调递增,在(x,+∞)上单调递减,所以x0是f(x)的唯一极值点令h(x)=hnx-x+1,则当x>1时,h(x)=x-1<0,故h(x)在(1,+∞)内单调递减,从而当x>1时h(x) e,lna>1时,有f(lna)=aln(lna)-(lna-1)em 1时,nx

18.解:(1)由已知得10×(0.010+0.015+0.015+m+0.025+0.005)=1,所以m=0.030(2分)(2)平均数x=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71设中位数为n,则0.1+0.15+0.15+(n-70)×0.03=0.5,所以n==3≈73.33故可以估计该企业所生产口罩的质量指标值的平均数为71,中位数为73.33.(6分)(3)由频率分布直方图可知,质检人员所抽取的100个口罩中,一等品、二等品的个数分别为60,40所以由分层抽样的方法可知,从该企业所抽取的100个口罩中,抽出5个口罩,抽出一等品、二等品的个数分别为3,2,记这3个一等品分别为a,b,c,记这2个二等品分别为d,e,则从这5个口罩中抽取2个的所有可能结果为(a,b),(a,c),(a,d),(a,e),(b,c)(b,d),(b,e),(c,d),(c,e),(d,e),共10个,其中恰有1个口罩为一等品的结果有(a,d),(a,e),(b,d),(b,e),(c,d),(c,e),共6个故这2个口罩中恰好有1个口罩为一等品的概率P(12分

以上就是20192022英语周报高一35期答案，更多英语周报答案请关注本网站。