2022 英语周报 高一 牛津 48答案



10.【解析】座椅做匀速圆周运动的半径为R=r+Lsin a(3分)由牛顿第二定律得 gtan=mRa2(3分)两式联立解得atan a(3分)解得转盘转动的角速度为√3(3分)


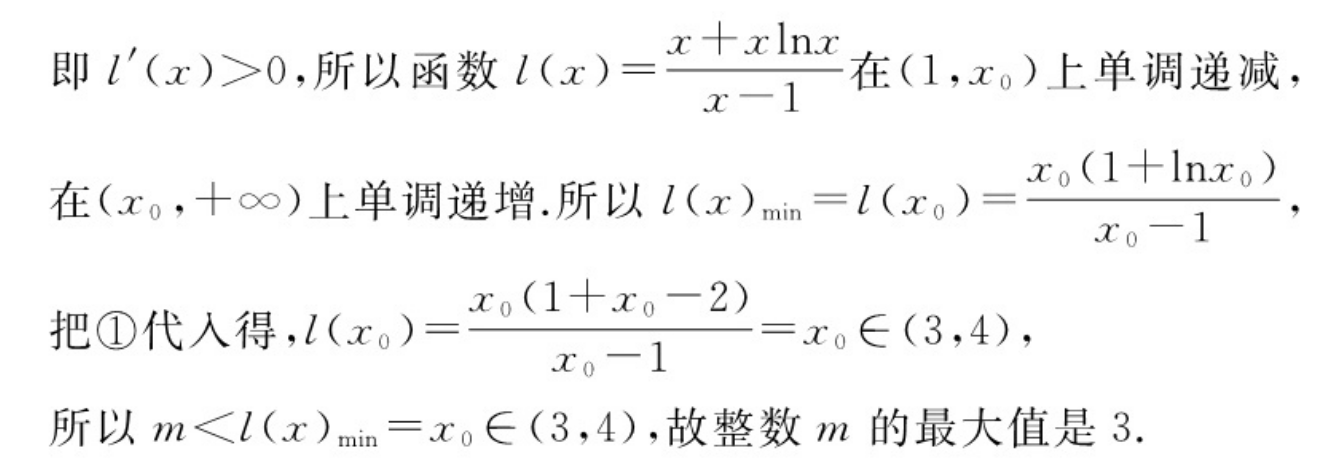
22.(1)f(x)的定义域是(0,+∞),令h(x)=a+lnx-ax(x>0),则f(x)=xh(x),故x>0时,f(x)≤0+h(x)≤0,因为h(1)0,h(x)≤0,所以h’(1)=0,因为h’(x)a,所以h'(1)1-a=0,所以a=1(2)证明:由(1)知f(x)=x+xlnx-x2,所以f(x)=2+lnx2x,令t(x)=2+lnx-2x(x>0),则t(x)2,当x∈0,)时,t'(x)>0,t(x)单调递增;当x∈0,t(x)单调递减.又t(e-2)<0,t0,t(1)=0,所以在0,)上存在唯一的x1,使得(x1)=0,在(,+∞上,(1)=0因为当x∈(0,x1)时,t(x)<0,即f(x)<0,当x∈(x1,1)时t(x)>0,即f(x)>0,当x∈(1,+∞)时,t(x)<0,即f(x)<0,所以f(x)存在唯一极小值点x(3)依题意得,g(x)=x+xlnx,所以g(x)>m(x-1)为raIn.x+xlnx>m(x-1),因为x>1,所以m
<对任意的x>
1恒成立,rIn.a令l(x)x>1,则1(x)=2=m令s(x)=x-1nx-2(x>1),则s(x)=10,所以函数s(x)在(1,十∞)上单调递增因为s(3)ln3<0,s(4)=2-1n4>0,所以方程s(x)=0在(1,+∞)上存在唯一的实数根x0,且x0∈(3,4),则s(x0)x0-lnx0-2=0,所以lnxo=x0-2①当1

以上就是2022 英语周报 高一 牛津 48答案,更多英语周报答案请关注本网站。






