2022英语周报九下外研版答案

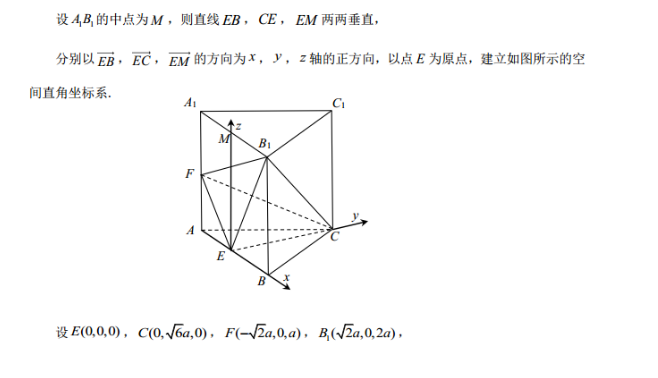
解:(1)证明:(法一)设AA1=2a24B=2Ea,EB1=√Ga,BB1点E为棱AB的中点eB=EB, =EB+BB, 2,EB⊥BB三棱柱ABC-ABC1的侧面ABA为平行四边形四边形ABB4为矩形点F为棱AA的中点FB=AF+AB=9a, FE=AF+AE=3aFB,2=EF2+EB2EF⊥EB三棱柱的底面ABC是正三角形,E为AB的中点,CE⊥ABCE⊥FBABc平面ABBA,FBc平面AB4,且AB,FB1必相交CE⊥平面ABAEFc平面ABBACE⊥EFEC∩EB1=EEF⊥平面CEB1(法二)先证明三棱柱ABC-ABC1是正三棱柱,与法一相同∠FAE=∠EBB=90°又:AB=A=25BE,点E,F分别为AB,A的中点BB,△FAE∽△EBB∠FEA+∠BEB,=90°∠FEB=90°又∵EF⊥CE,CEc平面CEB,EBC平面CEB1,且CE∩EB1=EEF⊥平面CEB…6分(2)解:(法一)由(1)可知CE⊥平面ABB1ACE⊥BB1CE⊥平面ABC三棱柱ABC-A1BC1是正三棱柱…8分设AB1的中点为M,则直线EB,CE,EM两两垂直分别以EB,EC,EM的方向为x,y,z轴的正方向,以点E为原点,建立如图所示的空间直角坐标系设E(000),C(0√6a,0),F(=√2an,0,a),B(√2a,0,2则EF=(-n0a),FC=(√5a,√6a,-a),FB1=(2√a,0.a)…8分ax+√6ay设平面CFB的一个法向量为n=(x,y,z),则2n2ax+0xy+az=0,两式相加并化简得√3x+y=0,不妨取x=1,y=-3,则z=-2√,即n=(,-√3,-2互).………10分√2a设直线EF与平面CFB所成角为6,则sEF则直线EF与平面CFB1所成角的大小为45°法二)由(1)知,在正三棱柱ABC-ABC1中,侧棱长为2a,底面正三角形ABC的边为2√a,高为√6a,EF=√则三棱柱ABC-ABC的体积HkA=×2√2 axv6ax2a=45a三棱锥F-AEC的体积V322ax、xaB,棱锥B一BC、“32+×0x2-25a四棱锥B-FCCA的体和N"3(a+20)x2√2ax√6a=25,易知用三棱柱ABC-ABC的体积减去上述三个棱锥的体积即为三棱锥E-CFB的体积则Fm-45-3,2万5a3+2a)=a3分设点E到平面CFB1的距离为h,应用勾股定理求得FB=3a,FC=3和BC=2a,易知等腰三角形CFB的底边上的高为√6a则三棱锥E-CFB的体积VFB322、5x√6xh=√ah0分由、5G=√5h,求得h=a设直线EF与平面CFB1所成角为0,则sin0则直线EF与平面CFB所成角的大小为45°12分(法三)由(1)知,在正三棱柱ABC-ABC1中,侧棱长为2a,底面正三角形ABC的边长为2√a,高为√6a,EF=√5a,EB=√Ga直接求得三棱锥C一BFB的体积Vm=3x2xxx=、5…8分设点E到平面CFB的距离为h,应用勾股定理求得FB1=3a,FC=3和BC=2易知等腰三角形CFB1的底边上的高为√6则三棱锥E一CFB的体积A=3x2×x60xh=、h10分由=√ah,求得h=÷a设直线EF与平面CFB所成角为,则sin0则直线EF与平面CFB所成角的大小为45°【命题意图】考查的知识点有线面垂直的性质与判定,空间向量,线面所成的角,勾股定理等.涉及到的思想方法主要有向量法,等体积法,数形结合思想,等价转化思想.检验的能力素养主要为空间想象能力,计算能力,综合应用数学知识与思想方法处理数学问题的能力

解:(1)∵AD=5,AC=8,△ACD的面积为10,∴×5×8sin∠DAC=103,∴sin∠DAC=3分∵0°<∠BAC<180°,AD平分∠BAC,∴0°<∠DAC<90°,∴∠DAC=60°……………4分在△ACD中,由余弦定理,得CD2=AD2+AC2-2xAC× ADxcos∠DAC=52+82-2×5×8×cs60=49CD=7(2)(法一)∵在△ACD中,由正弦定理,得CDsin∠ DAC sinCAD.sin∠DAC5sin60°8分在△ACD中,AD

以上就是2022英语周报九下外研版答案，更多英语周报答案请关注本网站。