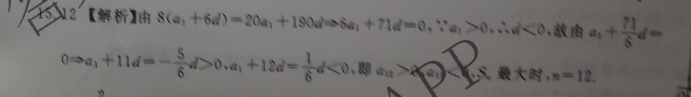21.【解析】(1)a=1时,f(x)=e-sinx-1g(r)=f(x)=e-cosr,h(x)=g(r)=e tsing, p(r)=h(r)=e+cosx>0故h(x)=g(x)为增函数,g(-2)<0,g(0)>0故3x∈(-,0),g(x0)=0,分在(x0,5)上,g(x)>0,g(x)=f(x)为增函数,且有唯一的零点x=0f(x)
0,故3x(∈(一2,x),(x)=04分故(-5,x)上,f(x)>0,f(x)单调递增,f(x)>f(-)>0,在(x1,0)上,f(x)<0,f(x)单调递减,f(x)>f(0)=0在(0,)上,f(x)>0,f(x)单调递增,f(x)>f(0)=06分综上所述,f(x)有唯一零点x=07分(2)由题f(0)≥0,则a-a20÷-1≤a<0或a21当-1≤a<0时,f(x)=ae-sinx--≥-e-sinx+1,令h(x)=-e+1(-丌≤x≤0),则A(x)=-c-c0sx<0,从而h(x)在[一2,0]上单调递减h(x)=m=h(0)=0,即-e-sinx+1≥0恒成立,从而f(x)≥0恒成立,分当a≥1时,由(1)知f(x)在[一2,0]上先增后减,又f(-)=ae-+1-1>0,且f(0)=a-1≥0,故f(x)≥0恒成立11分12分综上,a的取值范围为[一1,0)∪[1,+∞)
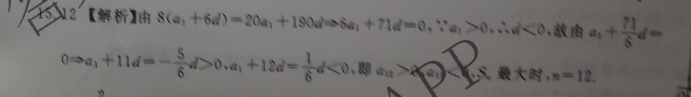
2【解】由8+0=20+1m+a=0,0,小,由a+0+1=-80+12-<0,即>最大时,m=12

以上就是2017-2018英语周报高二51答案,更多英语周报答案请关注本网站。