2022年九年级英语周报jxg答案

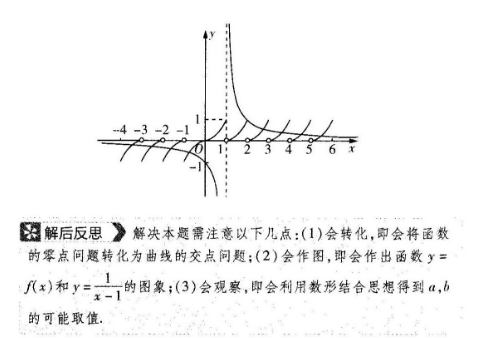
16.①④【试题情境】本题是综合性題目,属于探索创新情境,具体是数学探究情境【关键能力]本题考查逻辑思维能力、运算求解能力【解题思路】先确定函数的奇偶性和周期,再作图象,数形结合即可得解【解析】由∫(x)+f(-x)=0知f(x)是奇函数,因为当x<0时、f(1+x)=f(x),所以f(x)在(-∞,0)上是周期为1的周期函数.易知x=1不是F(x)的零点,当x≠1时,由F(x)=0,得f(x)=-1,作出函数y=f(x)和y=-;的大致图象如图所示,数形结合可知当这两个函数图象有8个交点时,①④正确解后反思》解决本题需注意以下几点:(1)会转化,即会将函数的零点问题转化为曲线的交点问题;(2)会作图,即会作出函数y=f(x)和y=,的图象;(3)会观察,即会利用数形结合思想得到a,b的可能取值

9.B【必备知识】本題考查的知识是“理解正弦函数在[0,2m]上的性质(如单调性、最大值和最小值、图象与x轴的交点等)”,“能画出函敫y=Asin(ωx+φ)的图象,了解参数A,a,9对函数图象变化的影响”【关键能力】本题考查运算求解能力【解析】解法一由題中图知函数∫(x)的最小正周期T=4×(-+=m22,由(=)=0得(+)=0,结合A>0,0<45分,得y=.所以f(x)=Asin(2x+).又f(0)=3,所以Asin=3,所以A=2,则f(x)=2in(2x+).因为xe[0所以2x+3∈3百],所以/(x)∈[-1,21,故选B=2,解法二由“五点作图法”,得解得。工所以0f(x)=Asin(2x+可).由f(0)=3,得Ain,=3,所以A=2,则f(x)-2i(2x+3.因为x∈(0.,所以2+3∈[·1,所以f(x)∈[-1,2],故选B

以上就是2022年九年级英语周报jxg答案，更多英语周报答案请关注本网站。