英语周报20192022高一第4期答案

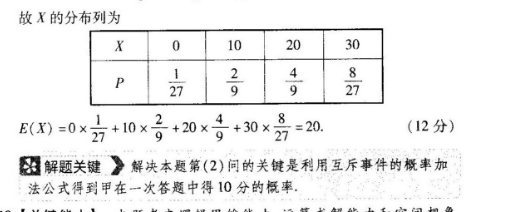
18.【试题情境】本题是应用性题目,属于生活实践情境,以垃圾分类知识竞賽为背景考查随机变量的分布列与数学期望等知识【关键能力】本题考查逻辑思维能力、数学建模能力和运算求解【解题思路】(1)首先通过题意分析出甲进入抢答环节包合两种情况,然后分别计算出每种情况的概率,相加即可得结果;(2)先列出X的所有可能取值,分别求出每个取值对应的概率,即可得X的分布列,再利用数学期望的计算公式求解即可解:(1)记“甲进入抢答环节”为事件A,则事件A包含“5道题全部答对”和“5道题答错1道,再抽取1道题回答正确”这两种情况,(2分)则3号e(号x*3需(4分)(2)由题意知,X的所有可能取值为0,10,20,30,(5分)记“抢答环节一次答题中甲得分”为事件B,则事件B包含甲抢到并答对和乙抢到并答错这两种情况故P(B)=2×3+2×3=3,(6分)则P(X=0)=Cx(3yx(3)=2(7分)P(x=10)=Cx3×(3)2=32(8分)P(x=20)=c×(3)×3=(9分)P(X=30)=C3x(2)2x()°(10分故X的分布列为故X的分布列为X4P087E(X)=0×⊥+10+204+30×21(12分)解题关键》解决本题第(2)问的关键是利用互斥事件的概率加法公式得到甲在一次答题中得10分的概率

21.【必备知识】本题考查的知识是“了解函数的单调性与导数的关系能利用导数研究函数的单调性,会求函数的单调区间(其中多项式函数不超过三次)【关键能力】本题考查逻辑思维能力、运算求解能力和创新能力f(0)【解题思路】(1)f(x)f(x)f(1)=(3+2b+c)e=0,n,f(1)=(a+b+c)eb,c的值(2)解法f(x)=(3f(x)≥g(x)在(0,+x)上恒成立+m≤(x+1)ee2-1在(0,+∞)上恒成立构造函数令h(x)(x+1)ee2-1讨论A(x)的革谓”(x)m的范围eN求导→+m的最大值解法二由(1)→f(x)=(f(x)≥g(x)在(0,+∞)上恒成立(x+1-m)e+m≥0在(0,+∞)上恒成立构逆函数求导令h(x)=(x+1-m)e'+m(x>0)一→h'(x)=(x+m52h(x)>0→h(x)在(0,+∞)上单调递增→h(x)>0→符合题意Lm>2h(x)的单调性→h(x)0→m-m+2≥0构造F=A(m-2)=m-c”2≥(m+2(m>2)v(m)的单调性(3)>0.(4)<0,且mN→m的最大值解:(1)由已知得∫'(x)=[ax2+(2a+b)x+b+c]e',(1分)且曲线y=f(x)过点(1,-e),(2分)f(0)=c=1,则{f(1)=(3a+2b+c)e=0,(4分)√f(1)=(a+b+c)e=-e,解得a=3,b=-5,c=1.(5分)(2)解法一由(1)得f(x)=(3x2-5x+1)e若f(x)≥g(x)在(0,+∞)上恒成立,则(3x2-5x+1)e'≥(3x2-6x+m)e2-m在(0,+∞)上恒成立,即(x+1)e'≥(e-1)m在(0,+∞)上恒成立,(6分)因为x>0,所以e-1>0,从而可得m≤(x+1)在(0,+)上恒成立e令h(x)(x+1)ee-1(x>0),则只需m≤h(x)(7分)h(x)=(C-x-2(x>0)令(x)=e-x-2(x>0),则φ'(x)=e'-1,因为x>0,所以φ'(x)=e'-1>0,(x)在(0,+∞)上单调递增,故方程φ(x)=0在(0,+∞)上若有根,则必唯(9分)因为(1)=e-1-2<0,q(2)=e2-4>0所以存在x0∈(1,2),使得φ(x)=e-x0-2=0,即h'(xn)=0,且当0 x0时,h'(x)>0,h(x)单调递增,则当x=x。时h(x)取最小值,h(x)。=h(x)(x0+1)e(10分)因为e-x0-2=0,所以e=x0+2,则h(x0)=x0+2因为x∈(1,2),所以h(x)e(3,4)(11分)因为m≤h(x)m,且m∈N,所以m≤3,故m的最大值为3.(12分)解法二由(1)得f(x)=(3x2-5x+1)e若f(x)≥g(x)在(0,+∞)上恒成立,则(3x2-5x+1)e'≥(3x2-6x+m)e'-m在(0,+∞)上恒成立,即(x+1-m)e'+m≥0在(0,+∞)上恒成立(7分)令h(x)=(x+1-m)e2+m(x>0),则h'(x)=(x+2-m)e'(x>0)若m≤2,则2-m≥0,又x>0,所以x+2-m>0,又x>0时e'>0,所以h'(x)>0,h(x)在(0,+∞)上单调递增因为当x=0时,(x+1-m)e'+m=1>0,所以当m≤2时,h(x)>0恒成立(9分)若m>2,则当x∈(0,m-2)时,h'(x)<0,h(x)单调递减,当x∈(m-2,+∞)时,h'(x)>0,h(x)单调递增,所以h(x)m=h(m-2)=m-e"2≥0,即lnm-m+2≥0.(10分令φ(m)=lnm-m+2(m>2),则φ'(m)=--10所以p(m)在(2,+∞)上单调递减,又q(3)=ln3-1>0,(4)=2ln2-2<0,且m∈N,所以m=3(11分)综上,m的最大值为3.(12分)团解后反思】(1)求解不等式恒成立问题时,可以分离参数,然后构造函数,将问题转化为新函数的最值问题,再结合题意求解参数的取值范围;(2)函数的零点存在但不可求时,常虚设零点,利用零点存在定理估计所设零点的范围,然后利用零点所满足的关系式进行代换

以上就是英语周报20192022高一第4期答案，更多英语周报答案请关注本网站。