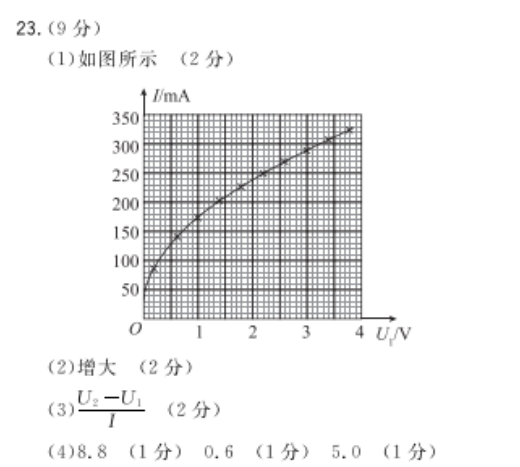

23.(9分)(1)如图所示(2分)I'mA350300鑘瞤瞤睍韁鑘輯250200鑘輖睴瞤睴瞤瞤1002(2)增大(2分)3)(2分)(4)8.8(1分)0.6(1分)5.0(1分)【命题意图】本题考查描绘小灯泡伏安特性曲线实验。【解题思路】(1)根据表中数据描点作图,如答图所示。(2)分析表中所测数据可知,随电压表V2示数不断增大,小灯泡电阻将增大,(3)毫安表两端电压为U2-U1,由欧姆定律得,毫安表内阻为rU2-U(4)由电阻的定义式R=—,可得小灯泡电阻R=T=.2500=8.8a;小灯泡消耗的电功率为P=3.45-2.20IU1≈0.6W;毫安表的内阻nA=0.200=5.0

解:(1)f(x)=e-4x-2的定义域为R,f(x)=e2-4,(1分)令f(x)<0,得x
0,得x>hn4,所以函数∫(x)在区间(-∞,2n2)上单调递减,在区间(2ln2,+∞)上单调递增所以函数f(x)在区间[0,2lm2]上单调递减,在区间[2m2,3]上单调递增.(2分)又f(0)=-1、f(3)=e-14,显然f(3)>f(0),(3分所以f(x)m=e3-14、f(x)m=f(2ln2)=2-8ln2.(4分(2)因为f(x)+x2-k≥0对任意x∈R恒成立所以e-4x-2+x2-k≥0对任意x∈R恒成立所以k≤e2+x2-4x-2对任意x∈R恒成立.(5分)令h(x)=e2+x2-4x-2,则h'(x)=e2+2x-4由于h"(x)=e+2>0,所以h(x)在R上单调递增.(6分)又(1)=6-2>0,(4)=e-12<0《所以存在唯一的x∈(4,1),使得h(x)=0,且当x∈(-∞,x)时,h(x)<0;当x∈(x,+)时,h(xn)>0.(7分)故h(x)在(-∞,x0)上单调递减,在(x0,+∞)上单调递增所以h(x)==h(x)=e0+x2-4x-2.(8分)又h'(x0)=0,即e0+2x0-4=0,所以e0=4-2x0所以h(x0)=e0+x2-4x0-2=4-2x0+x2-4x0-2=x2-6x0+2=(x0-3)2因为x∈(,1),所以h(x0)(。54),(10分)又因为k≤e+x2-4x-2对任意x∈R恒成立,所以k≤h(x0)又k∈Z,所以km=-3.(12分)

以上就是2021-2022 英语周报 高二 课标 20答案,更多英语周报答案请关注本网站。











