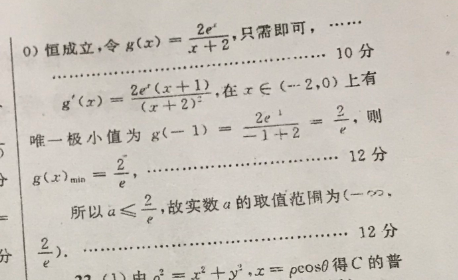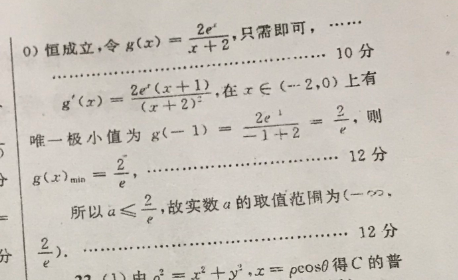
21.(1)f(x)=e+(x+为参1分1)(e'-a),当a>0时,令f(x)=0得x1=-1或x2C(3分(1)当0⊥时,x1>x2,此时令CD)>0,得x
na令f(x)<0,得-1
上时,f(x)的单调递增区间为(-∞,一),(lna,+∞),单调递减区间为(-1,lna).分(2)若Hx∈(-2,0),f(x)≤0恒成立,即x2+x)≤化简分离参数得a=x+2Vx∈(-22e2恒成立,令x+2,只需即可10分4(x)=2(x+1),在x∈(-2,0)上有+2)2,则唯一极小值为g1)+2212分(r)所以a≤二,故实数a的取值范围为(一012分s得C的普



18.【解】本题考查等差数列基本量的计算、求和公式以及等比中项的应用设等差数列{an}的公差为d,d>0选条件①6a1+4d=9解得a1=1,d=2,所以an=a1+(n-1)d=2n-1,n∈N因为111成等比数列1_1.1=34所以(2m-1)2=3(2t-1)因为t≤20,所以(2m-1)2≤11又m∈N',所以2m-1≤10,所以m≤5又(2m-1)2为3的倍数,且2m-1eN,所以t=14因为m
0,所以4m1(n-=a+(n-1)d12+4n-1即4|n+n(n-1)=[1+(n-1)d]2+4n-1整理得2(n-1)2=(n-1)2d,所以d=2,所以an=a1+(n-1)d=2n-1,n∈N整理得2{n-1)2=(n-1)2d,所以d=2,所以an=a1+(n-1)d=2n-1,n∈N因为1,1,1成等比数列所以=即所以(2m-1)2=3(2t-1).因为t≤20,所以(2m-1)2≤11又m∈N,所以2m-1≤10,所以m≤5.又(2m-1)2为3的倍数,且2m-1∈N‘,所以或514.因为m
0,所以(2+d)(2+2d)=2(2+6d),整理得d(d-3)=0,解得d=3(d=0舍去),所以an=a1+(n-1)d=3n-1,n∈N”因为成等比数列所以111a2;!所以(3m-1)2=5(3t-1因为t≤20,所以(3m-1)2≤295又m∈N,所以3m-1≤17,所以m≤6又(3m-1)2为5的倍数,且3m-1∈N‘,所以m=2,t=2因为m

以上就是2022~2028七年级英语周报答案,更多英语周报答案请关注本网站。