英语周报 2017-2018 高一 外研 17答案

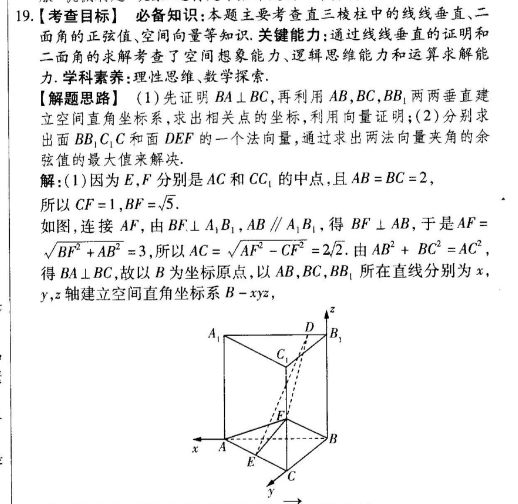
19.【考查目标】必备知识:本题主要考查直三棱柱中的线线垂直、二面角的正弦值、空间向量等知识.关键能力:通过线线垂直的证明和二面角的求解考查了空间想象能力、逻辑思维能力和运算求解能力学科素养:理性思维、数学探索【解题思路】(1)先证明BA⊥BC,再利用AB,BC,BB1两两垂直建立空间直角坐标系,求出相关点的坐标,利用向量证明;(2)分别求出面BB1C1C和面DEF的一个法向量,通过求出两法向量夹角的余弦值的最大值来解决解:(1)因为E,F分别是AC和C1的中点,且AB=BC=2所以CF=1,BF=√5.如图,连接AF,由BF⊥A1B1,AB∥AB,得BF⊥AB,于是AF=BF+ABF=3,所以AC=√AF-CF=2.由AB2+BC2=AC2,得BA⊥BC,故以B为坐标原点,以AB,BC,B1所在直线分别为x,y,z轴建立空间直角坐标系B-xy则B(0,0,0),E(1,1,0),F(0,2,1),BF=(0,2,1)设B1D=m(0≤m≤2),则D(m,0,2),于是DE=(1-m,1,-2)所以B.DE=0,所以BF⊥DE(2)易知面BB1C1C的一个法向量为n1=(1,0,0)设面DFE的法向量为n2=(x,y,2),n,又靂=(1-m,1,-2),E=(-1,1,1)所以(1-m)x+y-2z=0-x+y+z=0,令x=3,得y=m+1,z=2-m,于是,面DFE的一个法向量为n2=(3,m+1,2-m),所以cos(n1,n2〉=)2设面BCC与面DFE所成的二面角为6,则in6=√1-m(n1,m2),故当m=时,面BBCC与面DFE所成的二面角的正弦值最小为,即当B1D=时,面BB1C1C与面DFE所成的二面角的正弦值最小.【解題关键】本题求解关键是建立恰当的空间直角坐标系,确定相关点的坐标,再利用空间向量进行运算

18.【解析】(1)由题意可得,当物体在圆盘上随圆盘起转动时,圆盘对物体的静摩擦力提供向心力,所以随着圆盘转速的增大,物体受到的静摩擦力增大。当静摩擦力最大时,物体即将滑落,此时圆盘的角速度达到最大Nmo r(1分)N=mg(1分)联立解得a=入/-8=2rad/s(1分)(2)由题意可得,当物体滑到餐桌边缘时速度恰好减为零对应的餐桌半径取最小值。设物体在桌上滑动的位移为s物体在餐桌上做匀减速运动的婕速度大小为a,则a-m.=Amg'(1分)解得a=2.25m/s2(1分)物体在餐桌上滑动的初速度w=ar=3m/s(1分)由运动学公式得0-=-2as,可得5=2m(1分)由几何关系可得餐桌半径的最小值R=√P+了1分)(3)当物体滑离餐桌时,开始做平抛运动,平抛的初速度为物体在餐桌上滑动的末速度w,由题意可得v2-=一2as(1分)由于餐桌半径R=2r,所以x=r=1.5m(1分)可得w′=1,5m/s(1分)设物体做平抛运动的时间为t则h=gr2(1分)解得:-(2=0.4s(1分)本做平抛运动的水平位移为a2=vt=0.6m1分由题意可得L=s+s=2.1m(1分)

以上就是英语周报 2017-2018 高一 外研 17答案，更多英语周报答案请关注本网站。